
科目:初中数学 来源:湖南省邵阳市2018届九年级中考冲刺模拟数学试卷 题型:单选题
抛物线y=ax2+bx+c向右平移5个单位,再向上平移1个单位,得到的抛物线的解析式为y=-3(x-1)2+4,则抛物线y=ax2+bx+c的顶点坐标是( )
A. (6,3) B. (6,5) C. (-4,3) D. (-4,5)
查看答案和解析>>
科目:初中数学 来源:2018秋沪科版八年级数学上册第13章三角形中的边角关系 命题单元测试卷 题型:解答题
如图,已知∠C=∠1,∠2和∠D互余,BE⊥FD于点G.求证:AB∥CD.
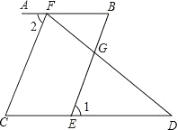
查看答案和解析>>
科目:初中数学 来源:陕西省2018年中考数学试卷 题型:解答题
问题提出
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在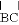 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).

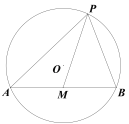

图① 图② 图③
查看答案和解析>>
科目:初中数学 来源:陕西省2018年中考数学试卷 题型:解答题
如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交与点G、H,若AB=CD,求证:AG=DH.
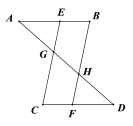
查看答案和解析>>
科目:初中数学 来源:陕西省2018年中考数学试卷 题型:单选题
如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是
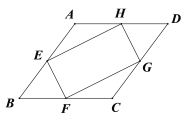
A. AB=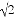 EF B. AB=2EF C. AB=
EF B. AB=2EF C. AB=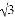 EF D. AB=
EF D. AB=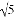 EF
EF
查看答案和解析>>
科目:初中数学 来源:北京海淀101上地实验学校2018届九年级9月月考数学试卷 题型:单选题
若二次函数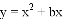 的图象的对称轴是经过点
的图象的对称轴是经过点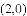
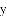
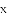
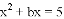 的解为( ).
的解为( ).
A. 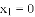 ,
,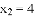 B.
B. 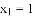 ,
,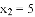 C.
C. 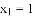 ,
,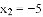 D.
D. 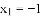 ,
,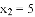
查看答案和解析>>
科目:初中数学 来源:湖南省邵阳市2018届九年级中考三模数学试卷 题型:填空题
如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E,F,则图中阴影部分的面积为________.
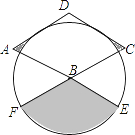
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com