
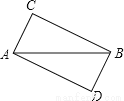
如图,△ABC≌△BAD,A和B,C和D分别是对应顶点,若AB=6cm,AC=4cm,BC=5cm,则AD的长为多少。
科目:初中数学 来源:2018人教版九年级数学下册练习:期中检测卷 题型:单选题
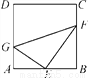
如图,在正方形ABCD中,点E为AB边的中点,点G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )
A. 3 B. 4 C. 5 D. 6
A 【解析】∵四边形ABCD是正方形, ∴∠A=∠B=90°, ∴∠AGE+∠AEG=90°,∠BFE+∠FEB=90°, ∵∠GEF=90°, ∴∠GEA+∠FEB=90°, ∴∠AGE=∠FEB,∠AEG=∠EFB. ∴△AEG∽△BFE, ∴ , 又∵AE=BE, ∴AE2=AG•BF=2, ∴AE= , ∴GF2=GE...查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册达标检测 第三章 变量之间的关系 题型:单选题
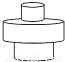
均匀地向如图的容器中注满水,能反映在注水过程中水面高度h随时间t变化的函数图象是( )
A. 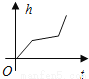 B.
B. 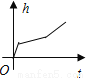 C.
C. 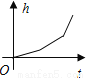 D.
D. 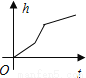
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型:填空题
如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的平分线FP相交于点P.若∠BEP=46°,则∠EPF=________°.
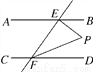
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型:单选题
如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为( )
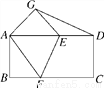
A. 5 B. 3 C. 2
C. 2 D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册4.2图形的全等练习 题型:单选题
下列四个图形中,全等的图形是( )
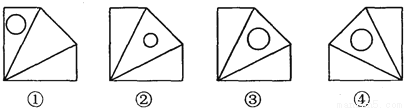
A. ①和② B. ①和③ C. ②和③ D. ③和④
D 【解析】试题分析:根据全等形的概念:能够完全重合的两个图形叫做全等形可得答案. 【解析】 ③和④可以完全重合,因此全等的图形是③和④. 故选:D.查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第五章达标检测卷 题型:解答题
(14分)如图,已知AB∥CD,AD∥BC,AC=15cm,BC=12cm,BE⊥AC于点E,BE=10cm.求AD和BC之间的距离.
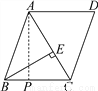
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第一章 整式的乘除 单元测试卷 题型:解答题
试说明:两个连续奇数的积加上1,一定是一个偶数的平方.
证明见解析. 【解析】试题分析:由题意设两个连续奇数为2n-1,2n+1,然后根据平方差公式进行证明. 试题解析:设两个连续奇数为2n?1,2n+1, 则(2n?1)(2n+1)+1=(2n)2?1+1=(2n)2 结果成立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com