练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    边数均为偶数的两正多边形的内角和为1800°．两个正多边形的边数分别为________．

    4和10或6和8
    分析：根据多边形的内角和公式可知，两正多边形的内角和为1800°，两正多边形的边数和为1800°÷180°+4=14，再根据两正多边形的边数均为偶数作答．
    解答：边数均为偶数的两正多边形的内角和为1800°，
    ∴两正多边形的边数和为1800°÷180°+4=14，
    ∴两个正多边形的边数分别为4和10或6和8．
    故答案为：4和10或6和8．
    点评：本题主要考查了多边形的内角和定理，注意两正多边形的边数和=两正多边形的内角和÷180+4．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    20、边数均为偶数的两正多边形的内角和为1800°．两个正多边形的边数分别为
    4和10或6和8
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    17、用三块正多边形的木板铺地，拼在一起并相交于一点的各边完全吻合，若其中两块木板的边数均为5，则第三块木板的边数为
    10
    ．

    查看答案和解析>>

    科目：初中数学 来源：三点一测丛书　九年级数学　上　（江苏版课标本） 江苏版课标本 题型：044

    操作示例

    对于边长均为a的两个正方形ABCD和EFGH，按如图甲所示的方式摆放，再沿虚线BD、EG剪开后，可以按图中所示的移动方式拼接为图甲中的四边形BNED．

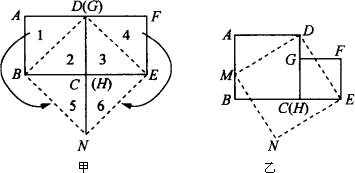
    从拼接的过程容易得到结论：

    ①四边形BNED是正方形；

    ②S正方形ABCD＋S正方形EFGH＝S正方形BNED．

    实践与探究

    (1)对于边长分别为a、b(a＞b)的两个正方形ABCD和EFGH，按如图乙所示的方式摆放，连结DE，过点D作DM⊥DE，交AB于点M，过点M作MN⊥DM，过点E作EN⊥DE，MN与EN相交于点N．

    ①证明：四边形MNED是正方形，并用含a、b的代数式表示正方形MNED的面积；

    ②在图乙中，将正方形ABCD和正方形EFGH沿虚线剪开后，能够拼接为正方形MNED．请简略说明你的拼接方法(类比图甲，用数字表示对应的图形)．

    (2)对于n(n是大于2的自然数)个任意的正方形，能否通过若干次拼接，将其拼接为一个正方形？请简要说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    边数均为偶数的两正多边形的内角和为1800°．两个正多边形的边数分别为______．

    查看答案和解析>>

    同步练习册答案