练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    判断题

    圆的对称轴是直径

    (　　)

    答案：F
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    (14分)已知抛物线y＝ax2＋bx＋c(a≠0)经过A(－2，0)、B(0，1)两点，且对称轴是y轴．经过点C(0，2)的直线l与x轴平行，O为坐标原点，P、Q为抛物线y＝ax2＋bx＋c(a≠0)上的两动点．

    【小题1】(1) 求抛物线的解析式；
    【小题2】(2) 以点P为圆心，PO为半径的圆记为⊙P，判断直线l与⊙P的位置关系，并证明你的结论；
    【小题3】(3) 设线段PQ＝9，G是PQ的中点，求点G到直线l距离的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    (14分)已知抛物线y＝ax2＋bx＋c(a≠0)经过A(－2，0)、B(0，1)两点，且对称轴是y轴．经过点C(0，2)的直线l与x轴平行，O为坐标原点，P、Q为抛物线y＝ax2＋bx＋c(a≠0)上的两动点．

    【小题1】(1) 求抛物线的解析式；
    【小题2】(2) 以点P为圆心，PO为半径的圆记为⊙P，判断直线l与⊙P的位置关系，并证明你的结论；
    【小题3】(3) 设线段PQ＝9，G是PQ的中点，求点G到直线l距离的最小值．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年福建省福州市九年级上学期期末考试数学卷 题型：解答题

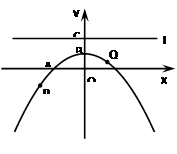
    (14分)已知抛物线y＝ax2＋bx＋c(a≠0)经过A(－2，0)、B(0，1)两点，且对称轴是y轴．经过点C(0，2)的直线l与x轴平行，O为坐标原点，P、Q为抛物线y＝ax2＋bx＋c(a≠0)上的两动点．

    【小题1】(1) 求抛物线的解析式；
    【小题2】(2) 以点P为圆心，PO为半径的圆记为⊙P，判断直线l与⊙P的位置关系，并证明你的结论；
    【小题3】(3) 设线段PQ＝9，G是PQ的中点，求点G到直线l距离的最小值．

    查看答案和解析>>

    科目：初中数学 来源：2011学年河北省考模拟考试数学卷 题型：选择题

    （本小题满分12分）

    如图，在平面直角坐标系中，顶点为（，）的抛物线交轴于点，交轴于，两点（点在点的左侧）， 已知点坐标为（，）。

    （1）求此抛物线的解析式；

    （2）过点作线段的垂线交抛物线于点， 如果以点为圆心的圆与直线相切，请判断抛物线的对称轴与⊙有怎样的位置关系，并给出证明；

    （3）已知点是抛物线上的一个动点，且位于，两点之间，问：当点运动到什么位置时，的面积最大？并求出此时点的坐标和的最大面积.

     

     

     

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案