
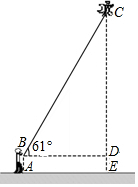
 小蓝周末去广场放风筝,如图,当风筝飞到点C处时的线长BC约为25m,此时小蓝正好站在点A处,并测得∠CBD=61°,牵引底端B距离地面1.5m,则此时风筝距离地面的高度CE约为23.3m(用科学计算器计算,结果精确到0.1m).
小蓝周末去广场放风筝,如图,当风筝飞到点C处时的线长BC约为25m,此时小蓝正好站在点A处,并测得∠CBD=61°,牵引底端B距离地面1.5m,则此时风筝距离地面的高度CE约为23.3m(用科学计算器计算,结果精确到0.1m). 科目:初中数学 来源: 题型:选择题
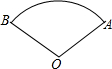 如图,爸爸从家(点O)出发,严沿着扇形AOB上OA→弧AB→BO的路径区匀速散步,设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )
如图,爸爸从家(点O)出发,严沿着扇形AOB上OA→弧AB→BO的路径区匀速散步,设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )| A. | 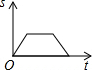 | B. |  | C. | 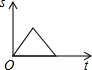 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com