
课题:两个重叠的正多边形,其中的一个绕某一个顶点旋转所形成的有关问题.
设旋转角∠A1A0B1=α(α<∠A1A0A2),![]() 3,
3,![]() 4,
4,![]() 5,
5,![]() 6所表示的角如图所示.
6所表示的角如图所示.
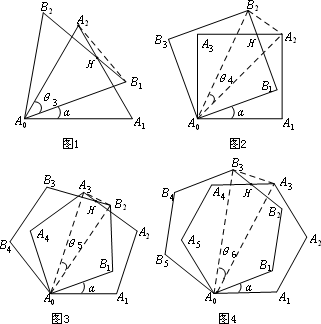
(1)用含α的式子表示角的度数:![]() 3=________,
3=________,![]() 4=________,
4=________,![]() 5=________;
5=________;
(2)图4中,连接A0H时,在不添加其他辅助线的情况下,是否存在与直线A0H垂直且被它平分的线段?若存在,请选择其中一个图给出证明;若不存在,请说明理由;
|
解:(1)60°-α,α,36°-α 3分 说明:每写对一个给1分 (2)存在下面就所选图形的不同分别给出证明: 下图中有直线AoH垂直平分A2B1,证明如下:
方法一: ∵△A0A1A2与△A0B1B2是全等的等边三角形, ∴A0A2=A0B1, ∴∠A0A2B1=∠A0B1A2 又∵∠A0A2H=∠A0B1H=60° ∴∠HA2B1=∠HB1A2 ∴A2H=B1H ∴点H在线段A2B1的垂直平分线上 又∵A0B1,∴点A0在线段A2B1的垂直平分线上 ∴直线A0H垂直平分A2B1 8分 方法二: 证明:∵△A0A1A2与△A0B1B2是全等的等边三角形, ∴A0A2=A0B1, ∴∠A0A2B1=∠A0B1B2 又∠A0A2H=∠A0B1H ∴∠HA2B1=∠HB1A2 ∴HA2=HB2 在△A0A2H与△A0B1H中 ∵A0A2=A0B1,HA2=HB1,∠A0A2H=∠A0B1H ∴△A0A2H≌△A0B1H ∴∠A2A0H=∠B1A0H ∴A0H是等腰三角形A2A0B1的顶角平分线 ∴直线A0H垂直平分A2B1 8分 下图中有直线A0H垂直平分A2B2,证明如下:
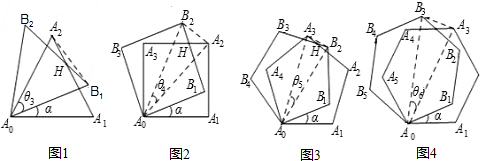
∵A0B2=A0A2 ∴∠A0B2A2=∠A0A2B2 又∵∠A0B2B2=∠A0A2A3=45°, ∴∠HB2A2=∠HA2B2 ∴HB2=HA2 ∴点H在线段A2B2的垂直平分线上 又∵A0B2=A0A2,∴点A0在线段A2B2的垂直平分线上 ∴直线A0H垂直平分A2B2 说明:(ⅰ)在图2中选用方法二证明的,参照上面的方法二给分; (ⅱ)选择图3或图4给予证明的,参照上述证明过程评分 (3)当n为奇数时, 当n为偶数时, (4)存在当n为奇数时,直线A0H垂直平分 当n为偶数时,直线A0H垂直平分 |


科目:初中数学 来源: 题型:
| 180 | n |
查看答案和解析>>
科目:初中数学 来源:2010年江西省赣州市定南三中初三毕业班教师专业考试数学试卷(解析版) 题型:解答题
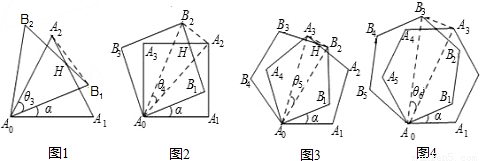
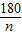 °);
°);查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《四边形》(08)(解析版) 题型:解答题

 °);
°);查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《三角形》(12)(解析版) 题型:解答题

 °);
°);查看答案和解析>>
科目:初中数学 来源:2010年江西省中考数学试卷(解析版) 题型:解答题

 °);
°);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com