解:解法1:∵AC=BC,CD⊥AB于D,
∴∠A=∠CBA,∠ACD=∠BCD,AD=BD=1,
根据已知条件有Rt△BCD≌Rt△BCE,
∴∠BCD=∠BCE,
∴∠ACD=∠BCD=∠BCE,
而A、C、E在一条直线上,
∴∠ACD+∠BCD+∠BCE=180°,
∴∠ACD=∠BCD=∠BCE=60°,
进而∠A=30°,
于是在Rt△ACD中,AC=2CD,AC
2=CD
2+AD
2,
∴4CD
2=CD
2+1,CD=

,
因此四边形BDCE的面积=2S
△BCD=2•

•BD•CD=

;
解法2:由对称性可知△CDB≌△CEB,
又AC=CB,CD⊥AB,
∴△ACD≌△CDB,
故S
四边形BDCE=

S
△ABE,
∵Rt△ABE中,BE=BD=1,AB=2,
∴∠A=30°,AE=

,
因此S
△ABE=

×

×1=

,即S
四边形BDCE=

.
分析:解法1:根据AC=BC,可知∠ACD=∠BCD,由△BCE与△BCD是关于BC成轴对称的,且A、C、E在一条直线上,可将∠ACD求出.在Rt△ACD中,可将CD的长求出,进而可求出△BCD的面积,根据四边形BDCE的面积为2S
△BCD,可将四边形BDCE的面积求出;
解法2:由题意可知△CDB≌△CEB≌△ACD,可得∠A=30°,从而可将△ABE的面积求出,根据S
△BDCE=

S
△ABE,从而可将四边形BDCE的面积求出.
点评:此题考查轴对称的基本性质,在解题过程中要注意一题多解.此题考查的计算技巧性很强,要注意对一些特殊三角形函数的应用.

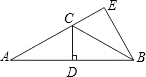 如图,在△ABC中,AB=2,AC=BC,CD⊥AB,垂足是D,△BCE与△BCD是关于BC成轴对称的,且恰好使A、C、E在一条直线上.求四边形BDCE的面积.
如图,在△ABC中,AB=2,AC=BC,CD⊥AB,垂足是D,△BCE与△BCD是关于BC成轴对称的,且恰好使A、C、E在一条直线上.求四边形BDCE的面积. ,
, •BD•CD=
•BD•CD= ;
; S△ABE,
S△ABE, ,
, ×
× ×1=
×1= ,即S四边形BDCE=
,即S四边形BDCE= .
. S△ABE,从而可将四边形BDCE的面积求出.
S△ABE,从而可将四边形BDCE的面积求出.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为