
已知抛物线y=-ax2+2ax=b与x轴的一个交点为A(-1,0),与y轴的正半轴交于点C.

(1)直接写出抛物线的对称轴,及抛物线与x轴的另一个交点B的坐标;
(2)当点C在以AB为直径的⊙P上时,求抛物线的解析式;
(3)坐标平面内是否存在点M,使得以点M和(2)中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.
|
解:(1)对称轴是直线: 说明:每写对1个给1分,“直线”两字没写不扣分. (2)如图,连接PC,∵点A、B的坐标分别是A(-1,0)、B(3,0), ∴AB=4.∴ 在Rt△POC中,∵OP=PA-OA=2-1=1, ∴ ∴b= 当 ∴ ∴ (3)存在 6分 理由:如图,连接AC、BC.设点M的坐标为
①当以AC或BC为对角线时,点M在x轴上方,此时CM∥AB,且CM=AB. 由(2)知,AB=4,∴|x|=4, ∴x=±4.∴点M的坐标为 说明:少求一个点的坐标扣1分. ②当以AB为对角线时,点M在x轴下方. 过M作MN⊥AB于N,则∠MNB=∠AOC=90°. ∵四边形AMBC是平行四边形,∴AC=MB,且AC∥MB. ∴∠CAO=∠MBN.∴△AOC≌△BNM.∴BN=AO=1,MN=CO= ∵OB=3,∴0N=3-1=2. ∴点M的坐标为 说明:求点M的坐标时,用解直角三角形的方法或用先求直线解析式, 然后求交点M的坐标的方法均可,请参照给分. 综上所述,坐标平面内存在点 说明:①综上所述不写不扣分;②如果开头“存在”二字没写,但最后解答全部正确,不扣分. |


科目:初中数学 来源: 题型:
 轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动.设动点运动的时间为t(秒).
轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动.设动点运动的时间为t(秒). (3)是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时E、F两点的坐标;若不存在,请说明理由.
(3)是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时E、F两点的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖南省祁阳县浯溪镇二中九年级下学期第一次月考考试数学卷 题型:单选题
.(13分)已知抛物线y=ax 2+bx+c经过O(0,0),A(4,0),B(3,)三点,连接AB,过点B作BC∥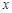 轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动.设动点运动的时间为t(秒).
轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动.设动点运动的时间为t(秒).
(1)求抛物线的解析式;
(2)记△EFA的面积为S,求S关于t的函数关系式,并求S的最大值,指出此时△EFA的形状;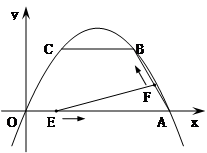 (3)是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时E、F两点的坐标;若不存在,请说明理由.
(3)是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时E、F两点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012届北京师大附中九年级上学期期中考试数学卷 题型:解答题
已知抛物线y=ax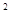 +bx+c与
+bx+c与 轴交于
轴交于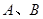 两点,若
两点,若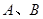 两点的横坐标分别是一元二次方程
两点的横坐标分别是一元二次方程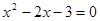 的两个实数根,与
的两个实数根,与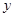 轴交于点
轴交于点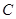 (0,3),
(0,3),
【小题1】(1)求抛物线的解析式;
【小题2】(2)在此抛物线上求点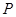 ,使
,使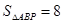 .
.
查看答案和解析>>
科目:初中数学 来源:2006年初中毕业升学考试(江苏无锡卷)数学(带解析) 题型:解答题
已知抛物线y=ax2+bx+c(a>0)的顶点是C(0,1),直线l:y=-ax+3与这条抛物线交于P、Q两点,与x轴、y轴分别交于点M和N。
(1)设点P到x轴的距离为2,试求直线l的函数关系式;
(2)若线段MP与PN的长度之比为3:1,试求抛物线的函数关系式。
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京师大附中九年级上学期期中考试数学卷 题型:解答题
已知抛物线y=ax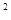 +bx+c与
+bx+c与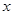 轴交于
轴交于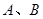 两点,若
两点,若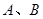 两点的横坐标分别是一元二次方程
两点的横坐标分别是一元二次方程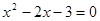 的两个实数根,与
的两个实数根,与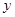 轴交于点
轴交于点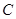 (0,3),
(0,3),
1.(1)求抛物线的解析式;
2.(2)在此抛物线上求点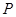 ,使
,使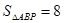 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com