直角三角形的两边长分别为16和12,则此三角形的外接圆半径是________.
10或8
分析:直角三角形的外接圆圆心是斜边的中点,那么半径为斜边的一半,分两种情况:①16为斜边长;②16和12为两条直角边长,由勾股定理易求得此直角三角形的斜边长,进而可求得外接圆的半径.
解答:由勾股定理可知:
①当直角三角形的斜边长为16时,这个三角形的外接圆半径为8;
②当两条直角边长分别为16和12,则直角三角形的斜边长=
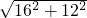
=20,
因此这个三角形的外接圆半径为10.
综上所述:这个三角形的外接圆半径等于8或10.
故答案为:10或8.
点评:本题考查的是直角三角形的外接圆半径,重点在于理解直角三角形的外接圆是以斜边中点为圆心,斜边长的一半为半径的圆.
