练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，把图（1）中的⊙A经过平移得到⊙O（如图（2）），如果图（1）中⊙A上一点P的坐标为（m，n），那么平移后在图（2）中的对应点p′的坐标为
    [     ]
    A.（m+2，n+1）
    B.（m-2，n-1）
    C.（m-2，n+1）
    D.（m+2，n-1）
    D
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    数学活动课上，甲、乙两位同学在研究一道数学题：“已知：如图1，在△ABC和△DEF中，∠A=∠D=90°，∠B=50°，∠E=32°，且BC=EF．试画直线m，l，使直线m将△ABC分成的两个小三角形与直线l将△DEF分成的两个小三角形分别相似，并标出每个小三角形各内角的度数．”
    甲同学是这样做的：如图2，使得两个直角三角形的斜边重合，以斜边中点0为圆心，OB长为半径作出辅助圆，根据到定点的距离等于定长的点在圆上，可知A、B（E）、C（F）、D在⊙0上．设BD所在的直线m与AC所在的直线l交于点G，根据同弧所对的圆周角相等，由∠ABC=50°，∠DEF=32°，易求得∠ABG=DFG=18°，再由∠A=∠D=90°，可求得∠AGB=∠DGF=72°，∠GCB=40°，∠BGC=108°，从而△AGB∽△DGF．△GBC∽△GEF．
    乙同学在甲同学的启发下，利用辅助圆又补充了其它分割方法．
    你看明白甲同学的分割方法了吗？请你仿照甲同学的方法，把这道题其它的所有分割方法补充完整．
    要求：不需写解答过程．如图2所示．利用辅助圆画出示意图，标明直线及每个小三角形各内角的度数即可．

    查看答案和解析>>

    科目：初中数学 来源：2009-2010学年北京市七年级下学期期末考试数学试卷（解析版） 题型：解答题

    阅读下列材料：                                        

    在学习小组，小明接到这样一个任务：把一个正方形分割成9个、10个和11个小正方形。为完成任务，小明先学习了两种简单的“基本分割法”。

    基本分割法1：如图①，把一个正方形分割成4个小正方形，即在原来1个正方形的基础上增加了3个正方形．

        基本分割法2：如图②，把一个正方形分割成6个小正方形，即在原来1个正方形的基础上增加了5个正方形．

     

     

    学习了上述两种“基本分割法”后，小明很从容地就完成了分割的任务：

    （1）把一个正方形分割成9个小正方形．

    方法一：如图③，把图①中的任意1个小正方形按“基本分割法2”进行分割，就可增加5个小正方形，从而分割成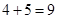（个）小正方形．

    方法二：如图④，把图②中的任意1个小正方形按“基本分割法1”进行分割，就可增加3个小正方形，从而分割成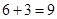（个）小正方形．

    （2）把一个正方形分割成10个小正方形．

    如图⑤，把图①中的任意2个小正方形按“基本分割法1”进行分割，就可增加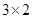个小正方形，从而分割成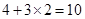（个）小正方形．

    请你参照上述分割方法解决下列问题（只要求画图，不用说明分割方法）：

    （1）请你替小明同学把图⑥给出的正方形分割成11个小正方形；

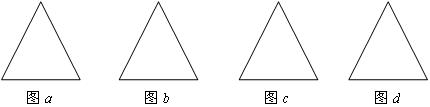
    （2）仿照基本分割法1：请把图a中的正三角形分割成4个小正三角形；

    （3）仿照基本分割法2：请把图b 中的正三角形分割成6个小正三角形；

    （4）分别把图c和图d中的正三角形分割成9个和10个小正三角形．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    数学活动课上，甲、乙两位同学在研究一道数学题：“已知：如图1，在△ABC和△DEF中，∠A=∠D=90°，∠B=50°，∠E=32°，且BC=EF．试画直线m，l，使直线m将△ABC分成的两个小三角形与直线l将△DEF分成的两个小三角形分别相似，并标出每个小三角形各内角的度数．”
    甲同学是这样做的：如图2，使得两个直角三角形的斜边重合，以斜边中点0为圆心，OB长为半径作出辅助圆，根据到定点的距离等于定长的点在圆上，可知A、B（E）、C（F）、D在⊙0上．设BD所在的直线m与AC所在的直线l交于点G，根据同弧所对的圆周角相等，由∠ABC=50°，∠DEF=32°，易求得∠ABG=DFG=18°，再由∠A=∠D=90°，可求得∠AGB=∠DGF=72°，∠GCB=40°，∠BGC=108°，从而△AGB∽△DGF．△GBC∽△GEF．
    乙同学在甲同学的启发下，利用辅助圆又补充了其它分割方法．
    你看明白甲同学的分割方法了吗？请你仿照甲同学的方法，把这道题其它的所有分割方法补充完整．
    要求：不需写解答过程．如图2所示．利用辅助圆画出示意图，标明直线及每个小三角形各内角的度数即可．

    查看答案和解析>>

    科目：初中数学 来源：北京模拟题 题型：解答题

    已知正方形ABCD的边长为1，直线l1∥直线l2，l1与l2之间的距离为1，l1、l2与正方形ABCD的边总有交点。
    （1）如图（1），当l1⊥AC于点A，l2⊥AC交边DC、BC分别于E、F时，求△EFC的周长；
    （2）把图（1）中的l1与l2同时向右平移x个单位，得到图（2），问△EFC与△AMN的周长的和是否随x的变化而变化，若不变，求出△EFC与△AMN的周长的和；若变化，请说明理由；
    （3）把图（2）中的正方形绕点O逆时针旋转α，得到图（3），问△EFC与△AMN的周长的和是否随α的变化而变化，若不变，求出△EFC与△AMN的周长的和；若变化，请说明理由。

    查看答案和解析>>

    同步练习册答案