

 ,
, ,
, );
);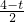 ,t),
,t),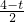 -t=
-t= ,
, ,
, ,
, 时,S=t•
时,S=t• =-
=- t2+2t;
t2+2t; 时,S=PQ2=(
时,S=PQ2=( )2=
)2= t2-6t+4;
t2-6t+4;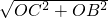 =2
=2 ,
, ①若CQ1=OQ1,过点Q1作Q1D⊥OC,
①若CQ1=OQ1,过点Q1作Q1D⊥OC, OC=2,
OC=2, ,
, ,
, ,
, 时,y=-2×
时,y=-2× +4=4-
+4=4- ,
, ,4-
,4- );
); ,4+
,4+ );
); ,x=0(舍去),
,x=0(舍去), ,-
,- );
); ,4-
,4- ),Q3(-
),Q3(- ,4+
,4+ ),Q4(
),Q4( ,-
,- ).
). (1)由题意可联立得方程组
(1)由题意可联立得方程组 ,解此方程组即可求得交点A的坐标;
,解此方程组即可求得交点A的坐标;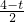 ,t),然后由当点N落在x轴上时,PN=PQ,求得t的值,然后分别从当0<t≤
,t),然后由当点N落在x轴上时,PN=PQ,求得t的值,然后分别从当0<t≤ 时与当
时与当 时去分析求解即可求得答案;
时去分析求解即可求得答案;

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
| k |
| x |
| 9 |
| 2 |
| k |
| x |
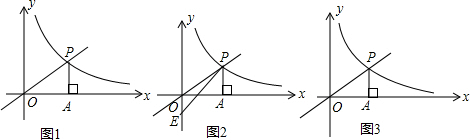
查看答案和解析>>
科目:初中数学 来源: 题型:
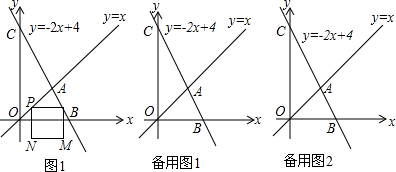
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 3 |
| k |
| x |
| k |
| x |
| k |
| x |
| k |
| x |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (k>0,x>0)交于点P,PA⊥x轴于A,S△PAO=
(k>0,x>0)交于点P,PA⊥x轴于A,S△PAO= .
. (x>0)上是否存在点Q,使S△QPO=S△MPO?若存在,求Q点的坐标;若不存在,请说明理由.
(x>0)上是否存在点Q,使S△QPO=S△MPO?若存在,求Q点的坐标;若不存在,请说明理由.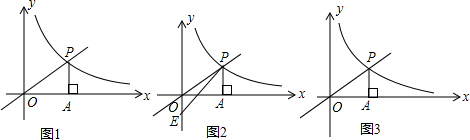
查看答案和解析>>
科目:初中数学 来源:2010-2011学年浙江省台州市三门中学九年级(上)月考数学试卷(10月份)(解析版) 题型:解答题
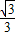 x+
x+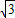 与两坐标轴交于A、B,以点M(1,0)为圆心,MO为半径作小⊙M,又以点M为圆心、MA为半径作大⊙M交坐标轴于C、D.
与两坐标轴交于A、B,以点M(1,0)为圆心,MO为半径作小⊙M,又以点M为圆心、MA为半径作大⊙M交坐标轴于C、D.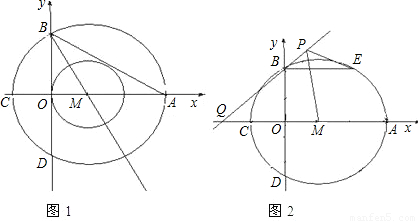
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com