练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    请你说明（）2与的区别．

     

    答案：
    解析：

    		在（)2中，被开方数a是一个非负数．

    它表示的意义是正数a的算术平方根的平方．

    即（）2＝a(a≥0)

    在中，被开方数a2中的a可取任何数．

    它表示的意义是：a2的算术平方根．

    即＝

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

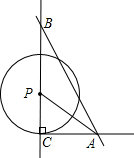    （2012•开平区一模）在Rt△ABC中，∠ACB=90°，AC=4cm，BC=8cm，以点P为圆心，以3cm长为半径的圆在直线BC上滑动．
    （1）如图，连接PA，若PA=PB时，请你判断⊙P与直线AC的位置关系，并说明理由；
    （2）当⊙P与直线AB的两个交点和圆心P为顶点的三角形是正三角形时，求PC的长；
    （3）设PC=x，请你直接写出⊙P与直线AB相交时x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•金平区模拟）如图1，在Rt△OAB中，∠AOB=90°，OA=OB=2
    		5
    ，点C、点D分别在OA、OB上，OC=OD=2．如图2，Rt△OAB绕点O顺时针旋转角θ（0°＜θ＜90°），得到△OMN．连接DN，若ND⊥OD，ON与CD交于点E．
    （1）求tanθ的值；
    （2）求DE的长；
    （3）延长DC交MN于点F，连接OF，请你确定线段OF与线段MN的关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•汉沽区一模）如图，一次函数y=kx+b的图象与反比例函数y=
    mx
    的图象交于A（2，1）、B（-1，n）两点．
    （1）求n的值；
    （2）一次函数的图象与x轴交于点C，与y轴交于点D，请你说明△OCD是等腰直角三角形．

    查看答案和解析>>

    科目：初中数学 来源：2009年北京市大兴区中考数学二模试卷（解析版） 题型：解答题

    （2009•大兴区二模）我们知道：将一条线段AB分割成大小两条线段AC、CB，若小线段CB与大线段AC的长度之比等于大线段AC与线段AB的长度之比，即．这种分割称为黄金分割，点C叫做线段AB的黄金分割点．类似地我们可以定义，顶角为36°的等腰三角形叫黄金三角形，其底与腰之比为黄金数，底角平分线与腰的交点为腰的黄金分割点．
    （1）如图1，在△ABC中，∠A=36°，AB=AC，∠ACB的角平分线CD交腰AB于点D，请你说明D为腰AB的黄金分割点的理由．
    （2）若腰和上底相等，对角线和下底相等的等腰梯形叫作黄金梯形，其对角线的交点为对角线的黄金分割点．如图2，AD‖BC，AB=AD=DC，AC=BD=BC，试说明O为AC的黄金分割点．
    （3）如图3，在Rt△ABC中，∠ACB=90°，CD为斜边AB上的高，∠A、∠B、∠ACB的对边分别为a、b、c．若D是AB的黄金分割点，那么a、b、c之间的数量关系是什么并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源：2005年福建省泉州市南安市初中学业质量检查数学试卷（解析版） 题型：解答题

    （2009•盐都区二模）南泉汽车租赁公司共有30辆出租汽车，其中甲型汽车20辆，乙型汽车10辆．现将这30辆汽车租赁给A，B两地的旅游公司，其中20辆派往A地，10辆派往B地，两地旅游公司与汽车租赁公司商定每天价格如下表：
      每辆甲型车租金（元/天）每辆乙型车租金（元/天） 
     A地 1000 800
     B地 900 600
    （1）设派往A地的乙型汽车x辆，租赁公司这30辆汽车一天共获得的租金为y（元），求y与x之间的函数解析式，并写出自变量x的取值范围；
    （2）若要使租赁公司这30辆汽车一天所获得的租金总额不低于26800元，请你说明有多少种分派方案，并将各种方案设计出来；
    （3）如果要使这30辆汽车每天获得的租金最多，请你为租赁公司提出合理的分派方案．

    查看答案和解析>>

    同步练习册答案