练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    一个正三角形绕它的中心旋转后如果能和原来的图形重合，那么它至少要旋转（      ）。
    120。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图①所示，将一个正三角形纸片沿着它的一条边上的高剪开，得到如图②所示的两个全等的Rt△ABC、Rt△DEF．
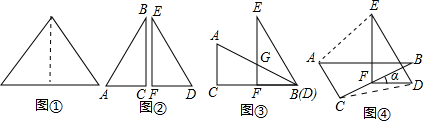
    精英家教网
    （1）根据正三角形的性质可知：在图②中，∠ABC=∠DEF=30°，AB=DE=2AC=2DF．由此请你归纳一下在含30°角的直角三角形中，30°角所对的直角边与斜边之间的关系：
    在含30°角的直角三角形中，30°角所对的直角边
     
    ；
    （2）将这两个直角三角形纸片按如图③放置，使点B、D重合，点F在BC上．固定纸片DEF，将△ABC绕点F逆时针旋转角α（0°＜α＜90°），使四边形ACDE为以ED为底的梯形（如图④所示），求此时α的值；
    （3）猜想图④中AE与CD之间的大小关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    27、在平面内，如果一个图形绕一个定点旋转一定的角度后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角称为这个图形的一个旋转角．例如：正方形绕着它的对角线的交点旋转90°后能与自身重合（如图），所以正方形是旋转对称图形，它有一个旋转角为90度．
    （1）判断下列命题的真假（在相应的括号内填上“真”或“假”）．
    ①等腰梯形是旋转对称图形，它有一个旋转角为180度．（
    假
    ）
    ②矩形是旋转对称图形，它有一个旋转角为180°．（
    真
    ）
    （2）填空：下列图形中，是旋转对称图形，且有一个旋转角为120°的是
    ①，③
    （写出所有正确结论的序号）：①正三角形；②正方形；③正六边形；④正八边形．
    （3）写出两个多边形，它们都是旋转对图形，都有一个旋转角为72°，并且分别满足下列条件
    ①是轴对称图形，但不是中心对称图形：
    如正五边形、正十五边形
    ；
    ②既是轴对称图形，又是中心对称图形：
    如正十边形、正二十边形
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2007•福州质检）如图，是三个边长相同的正三角形拼成的图形，该图形绕着O点旋转120°后能与本身重合．现将图中的正三角形分别涂上红、黄、蓝三种颜色，使它成为一个含颜色的图案．
    （1）如图①标记出了一种着色方案，请你在图②～⑥中标记出其余不同的着色方案；
    （2）若一个图案绕着O点旋转120°点后能得到另一个图案，就将它们归为同一类，试对（1）中所有的图案进行分类，并用线把同一类图案的序号连起来；
    （3）在（1）中，由图案①经过一次轴对称变换后能得到的图案的序号是
    4，5，6
    4，5，6
    ．

    查看答案和解析>>

    科目：初中数学 来源：2005年初中毕业升学考试（江苏南京卷）数学（带解析） 题型：解答题

    在平面内，如果一个图形绕一个定点旋转一定的角度后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角称为这个图形的一个旋转角．例如：正方形绕着它的对角线的交点旋转90°后能与自身重合（如图），所以正方形是旋转对称图形，它有一个旋转角为90°．

    （1）判断下列命题的真假（在相应括号内填上“真”或“假”）：
    ①等腰梯形是旋转对称图形，它有一个旋转角为180°．（        ）
    ② 矩形是旋转对称图形，它有一个旋转角为180°．（      ）
    （2）填空：下列图形中，是旋转对称图形，且有一个旋转角为120°的是            ．（写出所有正确结论的序号）：①正三角形；②正方形；③正六边形；④正八边形 ．   
    （3）写出两个多边形，它们都是旋转对称图形，都有一个旋转角为72°，并且分别满足下列条件：
    ①是轴对称图形，但不是中心对称图形；   ②既是轴对称图形，又是中心对称图形．

    查看答案和解析>>

    科目：初中数学 来源：2005年初中毕业升学考试（江苏南京卷）数学（解析版） 题型：解答题

    在平面内，如果一个图形绕一个定点旋转一定的角度后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角称为这个图形的一个旋转角．例如：正方形绕着它的对角线的交点旋转90°后能与自身重合（如图），所以正方形是旋转对称图形，它有一个旋转角为90°．

    （1）判断下列命题的真假（在相应括号内填上“真”或“假”）：

    ①等腰梯形是旋转对称图形，它有一个旋转角为180°．（         ）

    ② 矩形是旋转对称图形，它有一个旋转角为180°．（       ）

      （2）填空：下列图形中，是旋转对称图形，且有一个旋转角为120°的是             ．（写出所有正确结论的序号）：①正三角形；②正方形；③正六边形；④正八边形 ．   

    （3）写出两个多边形，它们都是旋转对称图形，都有一个旋转角为72°，并且分别满足下列条件：

    ①是轴对称图形，但不是中心对称图形；    ②既是轴对称图形，又是中心对称图形．

     

    查看答案和解析>>

    同步练习册答案