
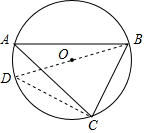
 ��ͼ����O�ǡ�ABC�����Բ���뾶ΪR����֪BC=a��AC=b��AB=c��
��ͼ����O�ǡ�ABC�����Բ���뾶ΪR����֪BC=a��AC=b��AB=c������ ��1����Բ�ܽǶ����ó���BCD=90�㣬��A=��D����Rt��BCD�У������Ǻ�������ó�sinD=$\frac{BC}{BD}$=$\frac{a}{2R}$���ó�$\frac{a}{sinD}$=2R�����$\frac{a}{sinA}$=2R�����������ɵó��𰸣�
��2���ɣ�1���ã�$\frac{a}{sinA}$=2R��ͬ����$\frac{b}{sin��ABC}$=2R�����ɵó����ۣ�
��3���ɣ�1���ã�$\frac{a}{sinA}$=2R��ͬ����$\frac{b}{sinB}$=2R��$\frac{c}{sinC}$=2R�����ɵó����ۣ�
��� ��1���⣺��BD�ǡ�O��ֱ����
���BCD=90�㣬
��Rt��BCD��sinD=$\frac{BC}{BD}$=$\frac{a}{2R}$��
��$\frac{a}{sinD}$=2R��
�ߡ�A=��D��
��sinA=sinD��
��$\frac{a}{sinA}$=2R��
��$\frac{a}{sinA}$-2R=2R-2R=0��
��2��֤�����ɣ�1���ã�$\frac{a}{sinA}$=2R��
ͬ����$\frac{b}{sin��ABC}$=2R��
��$\frac{a}{sinA}$=$\frac{b}{sin��ABC}$��
��3���⣺$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$���������£�
�ɣ�1���ã�$\frac{a}{sinA}$=2R��ͬ����$\frac{b}{sinB}$=2R��$\frac{c}{sinC}$=2R��
��$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$��
���� ������Բ���ۺ���Ŀ��������Բ�ܽǶ��������Ǻ����Ķ����Լ�Բ�����ʣ���������Բ�ܽǶ��������Ǻ��������ǽ������Ĺؼ���


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
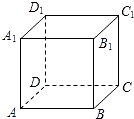 ��ͼ����������ABCD-A1B1C1D1���ⳤΪ1���ڡ��������dz�ͬʱ�ӵ�A����������ͬ���ٶȷֱ�������ǰ���У��ڼdz����е�·����AA1��A1D1�������dz����е�·����AB��BB1���������Ҷ���ѭ���¹��������еĵ�n+2���n�������ڵ�ֱ�߱����ǼȲ�ƽ��Ҳ���ཻ������n��������������ô���ڡ��������dz���������2013����ֱ�ֹͣ�������������嶥�㴦ʱ������֮��ľ����ǣ�������
��ͼ����������ABCD-A1B1C1D1���ⳤΪ1���ڡ��������dz�ͬʱ�ӵ�A����������ͬ���ٶȷֱ�������ǰ���У��ڼdz����е�·����AA1��A1D1�������dz����е�·����AB��BB1���������Ҷ���ѭ���¹��������еĵ�n+2���n�������ڵ�ֱ�߱����ǼȲ�ƽ��Ҳ���ཻ������n��������������ô���ڡ��������dz���������2013����ֱ�ֹͣ�������������嶥�㴦ʱ������֮��ľ����ǣ�������| A�� | 0 | B�� | 1 | C�� | $\sqrt{3}$ | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����ӣ����ڲ������Ž�Ŀ��������¼� | |
| B�� | Ϊ�˽�ij�ֽ��ܵƵ�ʹ��������ѡ��ȫ����� | |
| C�� | Ƶ������ͼ������ķ�ӳ����ı仯�������ʾ���ݱ仯���� | |
| D�� | 2016��������5.6�������б�ҵ���μ���ѧ���ԣ�Ϊ���˽���5.6������������ѧ�ɼ������г�ȡ200����������ѧ�ɼ�����ͳ�ƣ��������������������200����������ѧ�ɼ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ij����ʽ������������ʽ�Ľ⼯��ʾ�������ϣ���ͼ��ʾ�����������ʽ������ǣ�������
��ij����ʽ������������ʽ�Ľ⼯��ʾ�������ϣ���ͼ��ʾ�����������ʽ������ǣ�������| A�� | x��4��x��1 | B�� | x��4��x��-1 | C�� | x��4��x��-1 | D�� | x��4��x��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� | 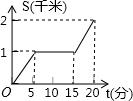 | D�� | 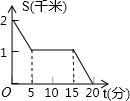 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
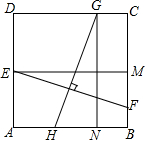 ��ͼ���ڱ߳�Ϊ4��������ABCD�У�EΪAD���е㣬FΪBC����һ���㣬��BF=t��0��t��2�����߶�EF�Ĵ�ֱƽ����GH�ֱ�CD��AB�ڵ�G��H����E��EM��BC�ڵ�M����G��GN��AB�ڵ�N��
��ͼ���ڱ߳�Ϊ4��������ABCD�У�EΪAD���е㣬FΪBC����һ���㣬��BF=t��0��t��2�����߶�EF�Ĵ�ֱƽ����GH�ֱ�CD��AB�ڵ�G��H����E��EM��BC�ڵ�M����G��GN��AB�ڵ�N���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
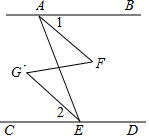 ��ͼ����֪��BAE+��AED=180�㣬��1=��2����ô��F=��G��Ϊʲô��
��ͼ����֪��BAE+��AED=180�㣬��1=��2����ô��F=��G��Ϊʲô���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com