
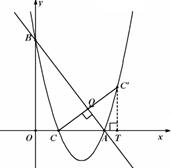
如图,已知抛物线 经过A(3,0)、B(0,4)
经过A(3,0)、B(0,4)
(1)求此抛物线的解析式;
(2)若抛物线与 轴的另一个交点为C,求点C关于直线AB的对称点
轴的另一个交点为C,求点C关于直线AB的对称点 的坐标;
的坐标;
(3)若点C是第二象限内一点,以点D为圆心的圆分别与 轴、
轴、 轴、直线AB相切于点E、F、H,问在抛物线的对称轴上是否存在一点P,使得
轴、直线AB相切于点E、F、H,问在抛物线的对称轴上是否存在一点P,使得 的值最大?若存在,求出该最大值;若不存在,请说明理由。
的值最大?若存在,求出该最大值;若不存在,请说明理由。

(1)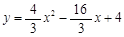 (2)(
(2)(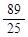 ,
,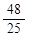 )(3)存在,
)(3)存在,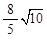
【解析】解:(1)由题意得: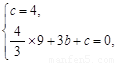 解得:
解得: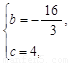
∴抛物线解析式为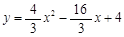 .················· 3分
.················· 3分
(2)令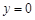 ,得
,得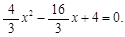
解得: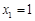 ,
,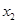 =3.
=3.
∴C点坐标为(1,0). ············· 4分
作CQ⊥AB,垂足为Q,延长CQ,使CQ=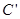 Q,则点
Q,则点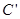
就是点C关于直线AB的对称点.
由△ABC的面积得:
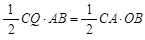 ,
,
∵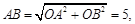 CA=2,
CA=2,
∴CQ= ,
,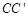 =
= .
························· 6分
.
························· 6分
作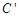 T⊥
T⊥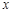 轴,垂足为T,则△
轴,垂足为T,则△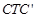 ∽△BOA.
∽△BOA.
∴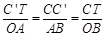 ∴
∴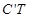 =
=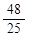 ,
, =
=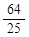
∴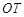 =1+
=1+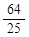 =
=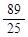 ∴
∴ 点的坐标为(
点的坐标为(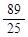 ,
,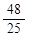 ) ··········· 8分
) ··········· 8分
(3)设⊙D的半径为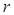 ,∴AE=
,∴AE=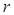 +3,BF=4-
+3,BF=4-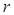 ,HB=BF=4-
,HB=BF=4-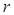 .
.
∵AB=5,且AE=AH,
∴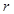 +3=5+4-
+3=5+4-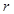 ,
,

∴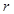 =3. ············· 10分
=3. ············· 10分
HB=4-3=1.
作HN⊥ 轴,垂足为N,
轴,垂足为N,
则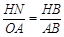 ,
, ,
,
∴HN=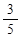 ,BN=
,BN=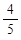 ,
,
∴H点坐标为(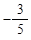 ,
,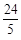 ).······ 12分
).······ 12分
根据抛物线的对称性,得PA=PC,
∵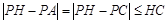 ,
,
∴当H、C、P三点共线时,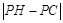 最大.
最大.
∵HC=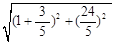 =
=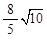 ,
,
∴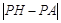 的最大值为
的最大值为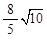 .
.
(1)用待定系数法求得抛物线解析式
(2)求出C点坐标,作CQ⊥AB,垂足为Q,延长CQ,使CQ=C'Q,则点C’就是点C关于直线AB的对称点.通过△ABC的面积,求出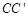 ,作
,作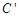 T⊥
T⊥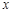 轴,垂足为T,通过△
轴,垂足为T,通过△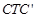 ∽△BOA.
求出
∽△BOA.
求出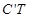 、
、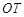 ,从而得出结论
,从而得出结论
(3)设⊙D的半径为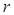 ,通过AB=5,且AE=AH,求得
,通过AB=5,且AE=AH,求得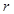 =3,作HN⊥
=3,作HN⊥ 轴,垂足为N,通过△HNB∽△OAB,求得H点坐标,根据抛物线的对称性,得PA=PC, 当H、C、P三点共线时,
轴,垂足为N,通过△HNB∽△OAB,求得H点坐标,根据抛物线的对称性,得PA=PC, 当H、C、P三点共线时,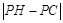 最大.利用勾股定理求出HC的长,即为最大值
最大.利用勾股定理求出HC的长,即为最大值


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
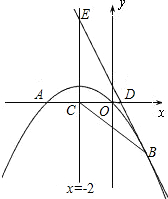 2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.
2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,查看答案和解析>>
科目:初中数学 来源: 题型:
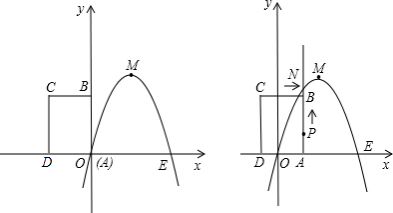
 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com