练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    某文具店销售甲、乙两种圆规，当销售5只甲种、1只乙种圆规，可获利润25元，销售6只甲种、3只乙种圆规，可获利润39元．

    （1）问该文具店销售甲、乙两种圆规，每只的利润分别是多少元？

    （2）在（1）中，文具店共销售甲、乙两种圆规50只，其中甲种圆规为a只，求文具店所获得利润P与a的函数关系式，并求当a≥30时P的最大值．

    （1）甲种圆规每只的利润是4元，乙种圆规每只的利润是5元；（2）220． 【解析】试题分析：（1）设文具店销售甲、乙两种圆规，每只的利润分别是x元、y元，根据题意“销售5只甲种、1只乙种圆规，可获利润25元，销售6只甲种、3只乙种圆规，可获利润39元”，列出的方程组，解方程组即可；（2）根据题意可以列出文具店所获利p与a的函数关系式，然后根据当a≥30，可以求得p的最大值即可． 试题解...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省2018届九年级上学期期末模拟数学试卷 题型：解答题

    (1)计算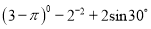： ； (2) 解方程：x2+4x+3=0．

    （1）；（2）， 【解析】试题分析： （1）代入30°角的正弦函数值，结合“0指数幂的意义”和“负指数幂的意义”计算即可； （2）根据方程的特点，用“因式分解法”解答即可. 试题解析： （1）原式= = =. （2）原方程可化为： ， ∴或， 解得： .

    查看答案和解析>>

    科目：初中数学 来源：山东省临朐县沂山风景区2017-2018学年七年级上期末模拟数学试卷 题型：单选题

    下列几何体中，属于棱柱的是（　　）

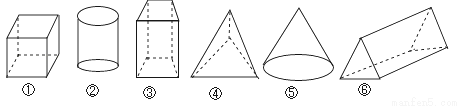
    A. ①③ B. ① C. ①③⑥ D. ①⑥

    C 【解析】所给几何体依次为：①棱柱；②圆柱；③棱柱；④棱锥；⑤圆锥；⑥棱柱，属于棱柱的有①③⑥， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017年湖南省郴州市中考数学模拟试卷 题型：单选题

    已知抛物线和直线l在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线x=﹣1，P1（x1，y1），P2（x2，y2）是抛物线上的点，P3（x3，y3）是直线l上的点，且x3＜﹣1＜x1＜x2，则y1，y2，y3的大小关系是（　　）

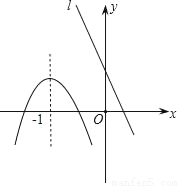
    A. y1＜y2＜y3 B. y2＜y3＜y1 C. y3＜y1＜y2 D. y2＜y1＜y3

    D 【解析】因为抛物线的对称轴为直线x=-1，开口向下，P1（x1，y1），P2（x2，y2）是抛物线上的点，且-1＜x1＜x2，根据二次函数的性质：在对称轴的右侧，y随x的增大而减小，可得y2＜ y1；P3（x3，y3）是直线l上的点，直线y随x的增大而减小，且x3＜-1，由图象可知，直线上x3对应的函数值y3大于-1对应的函数值，又因x=-1时，抛物线的顶点最高，可得y3最大，所以y2＜...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖南省郴州市中考数学模拟试卷 题型：单选题

    下列运算正确的是（　　）

    A. 3a2+5a2=8a4 B. a6•a2=a12 C. （a+b）2=a2+b2 D. （a2+1）0=1

    D 【解析】试题分析：A、原式合并同类项得到结果，即可做出判断； B、原式利用同底数幂的乘法法则计算得到结果，即可做出判断； C、原式利用完全平方公式展开得到结果，即可做出判断； D、原式利用零指数幂法则计算得到结果，即可做出判断． 【解析】 A、原式=8a2，故A选项错误； B、原式=a8，故B选项错误； C、原式=a2+b2+2ab，故C选项错误； ...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省中考数学模拟试卷 题型：解答题

    4x2﹣3=12x（用公式法解）．

    ， ． 【解析】试题分析：把方程化为一般形式后再利用公式法解方程即可. 试题解析： 原方程整理为：4x2﹣12x﹣3=0， ∵a=4，b=﹣12，c=﹣3， ∴△=144﹣4×4×（﹣3）=192＞0， 则x= = ， ∴， ．

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省中考数学模拟试卷 题型：单选题

    如图，?ABCD的周长为20cm，AC与BD相交于点O，OE⊥AC交AD于E，则△CDE的周长为（　　）

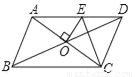
    A. 6cm B. 8cm C. 10cm D. 12cm

    C 【解析】试题分析：本题考查了平行四边形的性质、线段垂直平分线的性质以及三角形周长的计算；熟练掌握平行四边形的性质，运用线段垂直平分线的性质得出AE=CE是解决问题的关键。∵四边形ABCD是平行四边形，∴AB=DC，AD=BC，OA=OC， ∵?ABCD的周长为20cm， ∴AD+DC=10cm， 又∵OE⊥AC， ∴AE=CE， ∴△CDE的周长=DE+CE+DC=DE+AE+DC...

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年八年级上期末模拟数学试卷 题型：填空题

    如图，在Rt△ABC中，AB=BC=4，D为BC的中点，在AC边上存在一点E，连接ED，EB，则△BDE周长的最小值为________．

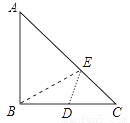
    【解析】过B作BO⊥AC于O，延长BO至B′，使B′O=BO，连接B′D，交AC于E，连接BE、B′C， ∴AC为BB′的垂直平分线， ∴BE=B′E，B′C=BC=4， 此时△BDE的周长为最小， ∵∠B′BC=45°， ∴∠BB′C=45°， ∴∠BCB′=90°， ∵D为BC的中点， ∴BD=DC=2， ∴B′D==， ∴△BDE的...

    查看答案和解析>>

    科目：初中数学 来源：安徽省2018届九年级上学期第二次月考数学试卷 题型：解答题

    如图，P、Q分别是正方形ABCD的边AB、BC上的点，且BP＝BQ，过点B作PC的垂线，垂足为点H，连接HD、HQ. （14分）

    (1)图中有________对相似三角形；

    (2)若正方形ABCD的边长为1，P为AB的三等分点，求△BHQ的面积；

    (3)求证：DH⊥HQ.

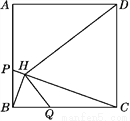
    （1）4；（2）（）证明见解析. 【解析】试题分析：(1)、根据角度之间的关系得出相似三角形；(2)、过点H作HE⊥BC于点E，根据P为三等分点得出BP=BQ=，根据Rt△PBC的勾股定理以及相似三角形求出BH的长度，根据Rt△BHC的勾股定理以及三角形相似求出HE的长度，从而得出△BHQ的面积；(3)、根据Rt△PBC∽Rt△BHC得出∠HBQ＝∠HCD，从而的得出△HBQ∽△HCD，即∠...

    查看答案和解析>>

    同步练习册答案