
 如图,将弧BC沿弦BC折叠交直径AB于点D,若AD=4,DB=8,则BC的长是________.
如图,将弧BC沿弦BC折叠交直径AB于点D,若AD=4,DB=8,则BC的长是________.
 =
=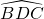 ,再根据在同圆或等圆中,等弧所对的圆周角相等可得∠BAC=∠BCD+∠CBD,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ADC=∠BCD+∠CBD,从而得到∠BAC=∠ADC,根据等角对等边可得AC=CD,过点C作CE⊥AD于E,根据等腰三角形三线合一的性质可得AE=DE=
,再根据在同圆或等圆中,等弧所对的圆周角相等可得∠BAC=∠BCD+∠CBD,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ADC=∠BCD+∠CBD,从而得到∠BAC=∠ADC,根据等角对等边可得AC=CD,过点C作CE⊥AD于E,根据等腰三角形三线合一的性质可得AE=DE= AD,然后利用△ACE和△CBE相似,根据相似三角形对应边成比例列式求出CE,在Rt△BCE中,利用勾股定理列式计算即可得解.
AD,然后利用△ACE和△CBE相似,根据相似三角形对应边成比例列式求出CE,在Rt△BCE中,利用勾股定理列式计算即可得解. =
=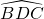 ,
, AD=
AD= ×4=2,
×4=2,
 =
= ,
, =
=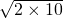 =2
=2 ,
, =
= =
=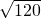 =2
=2 .
. .
.

科目:初中数学 来源:2013届浙江省杭州市绿城育华中学九年级12月月考数学试卷(带解析) 题型:填空题
如图,将弧BC沿弦BC折叠交直径AB于点D,若AD=5,DB=7,则BC的长是 .
查看答案和解析>>
科目:初中数学 来源:2013届浙江建德李家镇初级中学九年级上期末综合数学试卷(一)(带解析) 题型:填空题
如图,将弧BC 沿弦BC折叠交直径AB于点D,若AD=5,DB=7,则BC的长是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江宁波城区五校联考初三第一学期12月月考数学试卷(解析版) 题型:选择题
如图,将弧BC 沿弦BC折叠交直径AB于点D,若AD=6, DB=7,则BC的长是( )

A.  B.
B.
 C.
C.
 D.
D.

查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省杭州市九年级12月月考数学试卷(解析版) 题型:填空题
如图,将弧BC 沿弦BC折叠交直径AB于点D,若AD=5,DB=7,则BC的长是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com