
解:(1)∵DE∥BC,
∴

,
∴

,
∴y=

x(x>0且x≠3).
(2)作BH⊥AC,垂足为点H.
∵cosA=

,AB=5,
∴AH=

=

AC,
∴BH垂直平分AC.
∴△ABC为等腰三角形,AB=CB=5.

①当点D在BA边上时(两圆外切),如图(1)
易知:O
1O
2∥BC,∴O
1O
2=AO
1,
即

+

=5-

.
∵y=

x,
∴x=
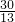
.
∵DE∥BC,
∴DE=AD=5-y,
∴DE=-

x+5.
∴DE=-

×
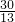
+5=
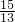
;
②当点D在BA延长线上时(两圆内切),如图(2)、(3),

易知O
1O
2∥BC,且O
1O
2=AO
1,
(ⅰ)如图(2),
∵O
1O
2=AO
1,
即

-

=5-

.
∵y=

x,
∴x=

.
∵DE∥BC,
∴DE=AD=y-5,
∴DE=

x-5.
∴DE=

×

-5=

.

(ⅱ)如图(3),
∵O
1O
2=AO
2,
即

-

=

-5,
∴x=10.
∵DE∥BC,
∴DE=AD=y-5,
∴DE=

x-5.
∴DE=

×10-5=

.

(3)①当∠EDF=∠B时,
易得:AD=DE=DF=DB,
∴AF⊥BC,
由cosA=cosC=

,AC=3,
∴FC=

,∴BF=

.

②当∠DEF=∠B时,如图(5)
易得:△DBF≌△EFC,
∴BF=

.
③当∠DFE=∠B时,如图(6)
∴
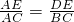
,
∵AB=5,BC=5,AC=3,
设DE=3k,DF=EF=5k,
∴

,

∴k=
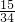
,
∴BF=5-3k=

.
综上所述:BF的长为:BF=

,

,

.
分析:(1)本题可利用DE∥BC,根据平行线分线段成比例定理,来求出x、y的函数关系式.
(2)本题要分两种情况:
①两圆外切,根据∠A的余弦值,如果过B作AC的垂线,不难得出△ABC为等腰三角形,因此AB=BC=5(也可用余弦定理求出BC的长).
那么△ADE也应该是等腰三角形,即AD=DE=5-y.
由于两圆外切,设以BD为直径的圆为⊙O
1,以CE为直径的圆为⊙O
2,那么O
1O
2就是梯形DECB的中位线,根据DE、BC的长即两圆的半径即可求出DE的长.
②两圆内切,此种情况又要分两种情况来求:
一:⊙O
2内切于⊙O
1,那么O
1O
2是两圆的半径差,可根据相似三角形ADE和AO
1O
2来求出DE的长.
二:⊙O
1内切于⊙O
2,同一.
(3)本题也要分三种情况:
①当∠ADE=∠FDE时,由于DE∥BC,那么∠ADE=∠FDE=∠DFB=∠B,即AD=DF=DE=DB,如果连接AF,那么DE必垂直平分AF,因此AF⊥CB,在直角三角形AFC中,由(2)知:∠A=∠C,因此根据AC的长和∠C的余弦值即可求出FC的长进而可求出BF的长.
②当∠DEF=∠B时,此时∠ADE=∠B=∠DEF,因此AB∥EF,四边形BDEF为平行四边形.因此△ADE≌△BDF,因此BF=BD=

AB,由此可求出BF的长.
③当∠DFE=∠B时,可根据相似三角形对应的腰和底成比例求出BF的长.
点评:本题考查了等腰三角形的判定和性质、圆与圆的位置关系、相似三角形的判定和性质等知识.

 .D为射线BA上的点(点D不与点B重合),作DE∥BC交射线CA于点E.
.D为射线BA上的点(点D不与点B重合),作DE∥BC交射线CA于点E. F的长;若不存在,请说明理由.
F的长;若不存在,请说明理由. 解:(1)∵DE∥BC,
解:(1)∵DE∥BC, ,
, ,
, x(x>0且x≠3).
x(x>0且x≠3). ,AB=5,
,AB=5, =
= AC,
AC,
 +
+ =5-
=5- .
. x,
x,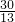 .
. x+5.
x+5. ×
×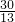 +5=
+5=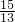 ;
;
 -
- =5-
=5- .
. x,
x, .
. x-5.
x-5. ×
× -5=
-5= .
.
 -
- =
= -5,
-5, x-5.
x-5. ×10-5=
×10-5= .
.
 ,AC=3,
,AC=3, ,∴BF=
,∴BF= .
.
 .
.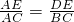 ,
, ,
,
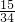 ,
, .
. ,
, ,
, .
. AB,由此可求出BF的长.
AB,由此可求出BF的长.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.