
因式分【解析】
(1)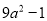 ; (2)
; (2)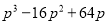
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:浙江省余姚市2018届九年级上学期期中考试数学试卷 题型:填空题
如图,在“3×3”网格中,有3个涂成黑色的小方格.若再从余下的6个小方格中随机选取1个涂成黑色,则完成的图案为轴对称图案的概率是______.
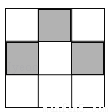
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:解答题
.在△ABC中,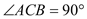 ,
, ,直线
,直线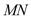 经过点
经过点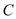 ,且
,且 于
于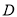 ,
, 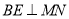 于
于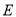 .
.
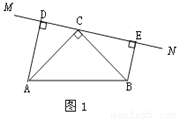
(1)当直线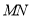 绕点
绕点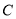 旋转到图1的位置时,
旋转到图1的位置时, 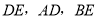 的数量关系是_________________ ,并请给出证明过程.
的数量关系是_________________ ,并请给出证明过程.
(2)当直线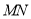 绕点
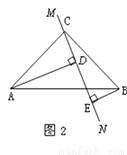
绕点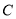 旋转到图2的位置时,
旋转到图2的位置时, 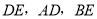 的数量关系是_________________ (直接写出结果)。
的数量关系是_________________ (直接写出结果)。
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:解答题
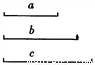
作图题: (1)已知:如图,线段a、b、c.
求作:ΔABC,使得BC=a,AC=b,AB=c.(保留作图痕迹,不写作法)
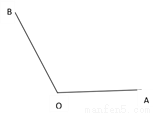
(2)求作:∠AOB的平分线OC.(不写作法,保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:填空题
如图是两个全等三角形,图中的字母表示三角形的边长,那么根据图中提供的信息可知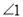 的度数为__________.
的度数为__________.


查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:单选题
如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
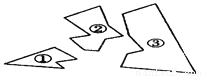
A. 带①去 B. 带②去 C. 带③去 D. 带①和②去
C 【解析】试题解析:A、带①去,仅保留了原三角形的一个角和部分边,不能得到与原来一样的三角形,故A选项错误; B、带②去,仅保留了原三角形的一部分边,也是不能得到与原来一样的三角形,故B选项错误; C、带③去,不但保留了原三角形的两个角还保留了其中一个边,符合ASA判定,故C选项正确; D、带①和②去,仅保留了原三角形的一个角和部分边,同样不能得到与原来一样的三角形,故D...查看答案和解析>>
科目:初中数学 来源:北京市海淀区2017-2018学年第一学期七年级期末考试数学参考样题 题型:填空题
已知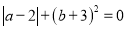 ,则
,则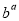 =__________.
=__________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期末检测题(一) 题型:解答题
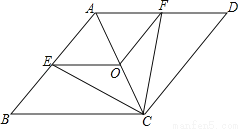
已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com