
解:已知:梯形ABCD 中,AD//BC,BC>AD,E、F分别为对角线BD、AC的中点,求证:EF//AD//BC,且EF= (BC-AD).
(BC-AD).
证明:延长EF交CD与N,延长FE交AB于M,连接DF并延长交BC于G.
∵AD//BC,
∴∠DAF=∠FCG,∠ADF=∠CGF.
又AF= CF,
∴△ADF≌△CGF.
∴DF=GF.
∵E是BD的中点.
∴EF为△DBG的中位线.
∴EF//BG,又AD//BC
∴EF//AD//BC.
∴E、F分别是BD、AC的中点,且EF//AD//BC.
∴MN为梯形ABCD的中位线,MN= (AD+BC).
(AD+BC).
又ME= AD= FN.
AD= FN.
∴EF= MN-MB-FN= (AD+BC)-
(AD+BC)- AD-
AD- AD=
AD=  (BC-AD).
(BC-AD).
∴梯形对角线中点的连线平行于两底. 并且等于两底差的一半。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 BE折叠,点A落在梯形对角线BD上的G处,EG的延长线交直线BC于点F.
BE折叠,点A落在梯形对角线BD上的G处,EG的延长线交直线BC于点F.查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(湖北宜昌卷)数学(带解析) 题型:解答题
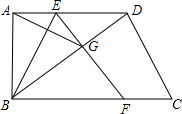
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E为底AD上一点,将△ABE沿直线BE折叠,点A落在梯形对角线BD上的G处,EG的延长线交直线BC于点F.
(1)点E可以是AD的中点吗?为什么?
(2)求证:△ABG∽△BFE;
(3)设AD=a,AB=b,BC=c
①当四边形EFCD为平行四边形时,求a,b,c应满足的关系;
②在①的条件下,当b=2时,a的值是唯一的,求∠C的度数.
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:解答题
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E为底AD上一点,将△ABE沿直线BE折叠,点A落在梯形对角线BD上的G处,EG的延长线交直线BC于点F.
(1)点E可以是AD的中点吗?为什么?
(2)求证:△ABG∽△BFE;
(3)设AD=a,AB=b,BC=c
①当四边形EFCD为平行四边形时,求a,b,c应满足的关系;
②在①的条件下,当b=2时,a的值是唯一的,求∠C的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com