某景点的门票价格如表:购票人数/人1-5051-100100以上每人门票价/元12108某校七年级两班计划去游览该景点.其中班人数多于50人且少于100人.如果两班都以班为单位单独购票.则一共支付1118元,如果两班联合起来作为一个团体购票.则只需花费816元．(1)两个班各有多少名学生?(2)团体购票与单独购票相比较.两个班各节约了多少钱? 题目和参考答案——青夏教育精英家教网—

某景点的门票价格如表：

购票人数/人	1～50	51～100	100以上
每人门票价/元	12	10	8

某校七年级（1）、（2）两班计划去游览该景点，其中（1）班人数少于50人，（2）班人数多于50人且少于100人，如果两班都以班为单位单独购票，则一共支付1118元；如果两班联合起来作为一个团体购票，则只需花费816元．

（1）两个班各有多少名学生？

（2）团体购票与单独购票相比较，两个班各节约了多少钱？

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：山东省东营市2018届数学中考一模试卷 题型：解答题

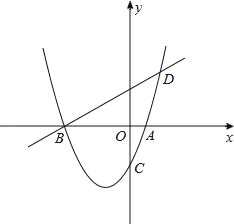
如图，已知抛物线y=ax2+bx﹣2（a≠0）与x轴交于A、B两点，与y轴交于C点，直线BD交抛物线于点D，并且D（2，3），tan∠DBA=．

（1）求抛物线的解析式；

（2）已知点M为抛物线上一动点，且在第三象限，顺次连接点B、M、C、A，求四边形BMCA面积的最大值；

（3）在（2）中四边形BMCA面积最大的条件下，过点M作直线平行于y轴，在这条直线上是否存在一个以Q点为圆心，OQ为半径且与直线AC相切的圆？若存在，求出圆心Q的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源：广东省湛江市廉江市2017-2018学年七年级下学期期末考试数学试卷 题型：单选题

若m是任意实数，则点M（m2+2，﹣2）在第（　　）象限．

A. 一 B. 二 C. 三 D. 四

查看答案和解析>>

科目：初中数学 来源：华东师大版九年级数学上册第23章综合能力检测卷 题型：单选题

（2017湖南株洲）如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点（Brocard point）是法国数学家和数学教育家克洛尔（A．L．Crelle 1780﹣1855）于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡（Brocard 1845﹣1922）重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（）

A. 5 B. 4 C. 3+ D. 2+

查看答案和解析>>

科目：初中数学 来源：华东师大版九年级数学上册第23章综合能力检测卷 题型：单选题

已知△ABC的三边长分别为6 cm，7.5 cm，9 cm，△DEF的一边长为4 cm，当△DEF的另外两边长是下列哪一组时，这两个三角形相似（）

A. 2 cm，3 cm B. 4 cm，5 cm C. 5 cm，6 cm D. 6 cm，7 cm

查看答案和解析>>

科目：初中数学 来源：河南省商丘市柘城县2017-2018学年七年级下学期期末考试数学试卷 题型：单选题

某校在“创建素质实践行”活动中组织学生进行社会调查，并对学生的调查报告进行了评比．如图是将某年级60篇学生调查报告的成绩进行整理，分成5组画出的频数分布图．已知从左到右4个小组的百分比分别是5%，15%，35%，30%，那么在这次评比中被评为优秀的调查报告有（分数大于或等于80分为优秀，且分数为整数）（　　）