练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

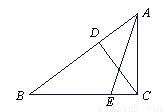
    已知在△ABC中,∠ACB=90°,CD⊥AB于D,BE:AB=3：5,若CE=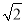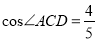， ，求tan∠AEC值及CD的长.

    tan∠AEC=3, CD= 【解析】【解析】 在RT△ACD与RT△ABC中 ∵∠ABC+∠CAD=90°, ∠ACD+∠CAD=90°∴∠ABC=∠ACD, ∴cos∠ABC=cos∠ACD= 在RT△ABC中， 令BC=4k,AB=5k 则AC=3k 由 ,BE=3k 则CE=k,且CE= 则k=，AC=3 ∴RT△ACE中，tan∠AEC==3 ∵RT...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：河北省唐山市路北区2017-2018学年七年级（上）期末复习数学试卷 题型：填空题

    若（a﹣2）2+|b+3|=0，则（a+b）2014=________．

    1 【解析】试题解析： ∴a=2，b=?3， 故答案为：1.

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省中考数学模拟试卷 题型：解答题

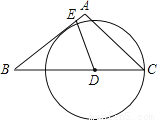
    如图，在等腰△ABC中，AB=AC=5，BC=6，点D为BC边上一动点（不与点B重合），过D作射线DE交AB边于E，使∠BDE=∠A，以D为圆心、DC的长为半径作⊙D．

    （1）设BD=x，AE=y，求y关于x的函数关系式，并写出定义域．

    （2）当⊙D与AB边相切时，求BD的长．

    （3）如果⊙E是以E为圆心，AE的长为半径的圆，那么当BD的长为多少时，⊙D与⊙E相切？

    (1) y=5-x（0＜x≤）；(2) ；(3) 或． 【解析】 试题分析：（1）通过相似三角形△BDE∽△BAC的对应边成比例得到，把相关线段的长度代入并整理得到y=5-x（0＜x≤）； （2）如图，假设AB与⊙D相切于点F，连接FD．通过相似三角形△BFD∽△BGA的对应边成比例得到．DF=6-BD，由勾股定理求得AG=4，BA=5，所以把相关线段的长度代入便可以求得BD的长...

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省中考数学模拟试卷 题型：单选题

    如图，四边形ABCD为圆内接四边形，E为DA延长线上一点，若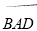的度数为70°，则∠BAE的度数为（　　）

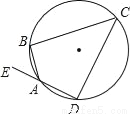
    A. 140° B. 70° C. 35° D. 20°

    C 【解析】试题解析：∵的度数为 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省中考数学模拟试卷 题型：单选题

    如图，小手盖住的点的坐标可能为（ ）

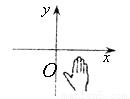
    A. （5，2） B. （–6，3） C. （–4，–6） D. （3，–4）

    D 【解析】小手盖住的点为第四象限内的点，横坐标为正数，纵坐标为负数，故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年天津109中中考数学模拟试卷 题型：填空题

    如图在△ABC中，AB=2，AC=4，将△ABC绕点C按逆时针方向旋转得到△A′B′C，使CB′∥AB，分别延长AB，CA′相交于点D，则线段BD的长为___________．

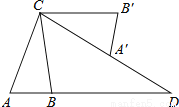
    6 【解析】试题解析：∵将△ABC绕点C按逆时针方向旋转得到△A′B′C， ∴AC=CA′=4，AB=B′A′=2，∠A=∠CA′B′， ∵CB′∥AB， ∴∠B′CA′=∠D， ∴△CAD∽△B′A′C， ∴， ∴， 解得AD=8， ∴BD=AD-AB=8-2=6．

    查看答案和解析>>

    科目：初中数学 来源：2017年天津109中中考数学模拟试卷 题型：单选题

    如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为（ ）

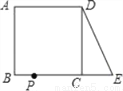
    A. 3 B. 5 C. 7 D. 3或7

    D 【解析】当P运动到BC的中点或者AD的中点时，△ABP和△DCE全等 此时，t=3或7.

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省中考数学模拟试卷 题型：填空题

    已知点P（a，b）在直线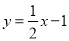上，点Q（﹣a，2b）在直线y=x+1上，则代数式a2﹣4b2﹣1= ．

    1． 【解析】 试题分析：先根据题意得出关于a的方程组，求出a，b的值代入代数式进行计算即可． 试题解析：∵点P（a，b）在直线上，点Q（﹣a，2b）在直线y=x+1上， ∴，解得， ∴原式=﹣4×﹣1=1．

    查看答案和解析>>

    科目：初中数学 来源：江苏省无锡市2017-2018学年七年级12月月考数学试卷 题型：解答题

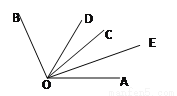
    如图，已知∠AOC=40°，∠BOC=80°，OD平分∠AOB.

    求（1）∠COD的度数；

    （2）若OE是∠AOC的角平分线，求∠EOD的度数.

    (1) ∠COD=20°；(2)∠DOE=40°. 【解析】试题分析：（1）先利用角的和求出∠AOB的度数，然后利用角平分线的定义求出∠AOD的度数，最后利用∠COD＝∠AOD－∠AOC求出∠COD的度数； （2）先利用角平分线的定义求出∠COE的度数，然后利用∠DOE＝∠DOC＋∠COE即可求出∠DOE的度数． 试题解析： 【解析】 （1）∵∠AOC＝40°，∠BOC＝...

    查看答案和解析>>

    同步练习册答案