
 如图,将边长为3+
如图,将边长为3+ 的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1,则重叠部分的面积为________.
的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1,则重叠部分的面积为________.

 ,
, ∠FDB=45°
∠FDB=45° =
= ,
, ,
, AD•DN=
AD•DN= ×1×
×1× =
= ,
, -1=2+
-1=2+ ,
,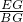 =
= ,
, x,
x, x=2+
x=2+ ,
,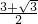 ,
,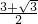 ,
, BD•EG=
BD•EG= ×(2+
×(2+ )×
)×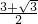 =
= ,
, =
= +1,
+1, ,
, ,
, -
- ×1×
×1× =
= .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
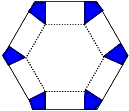 如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为查看答案和解析>>
科目:初中数学 来源: 题型:
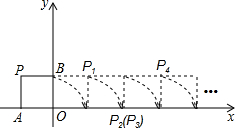 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2009次,点P依次落在点P1,P2,P3,P4,…,P2009的位置,则P2009的坐标为
如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2009次,点P依次落在点P1,P2,P3,P4,…,P2009的位置,则P2009的坐标为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com