
 如图:⊙O内切于边长为2的等边△ABC,分别以A、B、C为圆心,1为半径画弧,则图中阴影部分面积为________.
如图:⊙O内切于边长为2的等边△ABC,分别以A、B、C为圆心,1为半径画弧,则图中阴影部分面积为________. π-
π-
 解:过点A作AD⊥BC于D,圆心为点O,连接BO.
解:过点A作AD⊥BC于D,圆心为点O,连接BO. .
. -x,
-x, -x)2,
-x)2, ,
, ×BC×AD=
×BC×AD= ,
,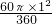 =
= -
- ,
, -π×
-π× =
= -
- ,
, -(
-( -
- )-(
)-( -
- )=
)= π-
π- .
. π-
π- .
.

科目:初中数学 来源: 题型:
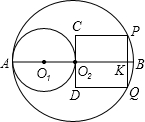 PQ⊥O1O2,交O1O2于点K,且PK=
PQ⊥O1O2,交O1O2于点K,且PK=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
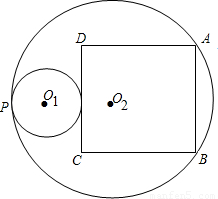
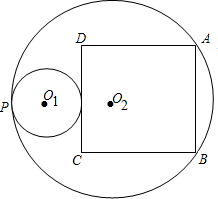 (2012•蕲春县模拟)如图⊙O1与⊙O2内切于点P,正方形ABCD的顶点A、B在⊙O2上,边CD与⊙O1相切,若⊙O1的直径是3,⊙O2的半径是5,求正方形的边长.
(2012•蕲春县模拟)如图⊙O1与⊙O2内切于点P,正方形ABCD的顶点A、B在⊙O2上,边CD与⊙O1相切,若⊙O1的直径是3,⊙O2的半径是5,求正方形的边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
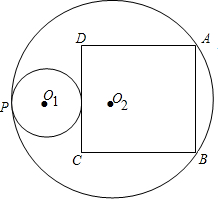 如图⊙O1与⊙O2内切于点P,正方形ABCD的顶点A、B在⊙O2上,边CD与⊙O1相切,若⊙O1的直径是3,⊙O2的半径是5,求正方形的边长.
如图⊙O1与⊙O2内切于点P,正方形ABCD的顶点A、B在⊙O2上,边CD与⊙O1相切,若⊙O1的直径是3,⊙O2的半径是5,求正方形的边长.查看答案和解析>>
科目:初中数学 来源:2012年湖北省黄冈市蕲春县三校联考九年级数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com