练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若A(a，b)，两点均在函数的图像上，且－1＜a＜0，则b－c的值为

    [　　]

    A．正数

    B．负数

    C．零

    D．非负数

    答案：B
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2012•昆山市二模）如图，已知点A的坐标为（2，4），在点A处有二只蚂蚁（忽略其大小），它们同时出发，一只以每秒1个单位的速度垂直向上爬行，另一只同样以每秒1个单位的速度水平向右爬行，t秒后，它们分别到达B、C处，连接BC．若在x轴上有两点D、E，满足DB=OB，EC=OC，则
    （1）当t=1秒时，求BC的长度；
    （2）证明：无论t为何值，DE=2AC始终成立；
    （3）延长BC交x轴于点F，当t的取值范围是多少时，点F始终在点E的左侧？（请直接写出结果，无需书写解答过程！）

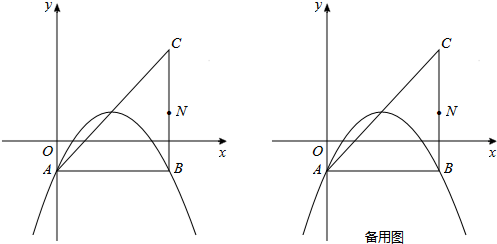
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•成都）在平面直角坐标系中，已知抛物线y=-
    1
    2
    x2+bx+c（b，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，-1），C的坐标为（4，3），直角顶点B在第四象限．
    （1）如图，若该抛物线过A，B两点，求该抛物线的函数表达式；
    （2）平移（1）中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q．
    （i）若点M在直线AC下方，且为平移前（1）中的抛物线上的点，当以M、P、Q三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点M的坐标；
    （ii）取BC的中点N，连接NP，BQ．试探究
    PQ
    NP+BQ
    是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某拱形门建筑的形状是抛物线，若取拱形门地面上两点的连线为x轴，它可以近似的用函数y=-
    297
    x2+4x    表示（单位：m）．
    （1）求拱形门的宽（地面上的两点之间的距离）；
    （2）求拱形门的高．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，某拱形门建筑的形状是抛物线．若取拱形门地面上两点的连线为x轴，它可以近似地用函数y=-
    297
    (x-97)2+194    表示（单位：m）．则拱形门的宽度大约是
    194
    194
    m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    选做题：如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在C、D之间有一点P，如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD之间的关系是否发生变化．若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？

    查看答案和解析>>

    同步练习册答案