练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．如图，在△ABC中，∠C=90°，∠B=30°，边AB的垂直平分线DE交AB于点E，交BC于点D，CD=3，则BC的长为（　　）
    A．6B．9C．10D．12

    分析 根据三角形内角和定理求出∠BAC，根据线段垂直平分线的性质得到AD=BD，求出∠BAD和∠CAD，根据直角三角形的性质解答即可．

    解答 解：∵∠C=90°，∠B=30°，
    ∴∠BAC=60°，
    ∵DE是AB的垂直平分线，
    ∴DB=DA，
    ∴∠BAD=∠B=30°，
    ∴∠CAD=30°，
    ∴AD=2CD=6，
    ∴DB=AD=6，
    ∴BC=3+6=9，
    故选：B．

    点评 本题考查的是直角三角形的性质、线段垂直平分线的性质，掌握线段垂直平分线上任意一点，到线段两端点的距离相等是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年福建省泉州市泉港区七年级3月教学质量检测数学试卷（解析版） 题型：单选题

    我国古代名著《九章算术》中有一题“今有凫起南海，七日至北海；雁起北海，九日至南海．今凫雁俱起，问何日相逢？”（凫：野鸭）设野鸭与大雁从北海和南海同时起飞，经过x天相遇，可列方程为（　 　）

    A. （9﹣7）x=1 B. （9+7）x=1 C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．化简求值：
    ①5（3a2b-ab2）-2（ab2+3a2b），其中 a=-2，b=-1．
    ②2m-{7n+[4m-7n-2（m-2n-3m）]-3m}，其中m=-3，n=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，在平面直角坐标系中，点A在第一象限，且OA=6，与x轴相切于点B，
    且∠AOB=30°
    （1）求⊙A的半径长；
    （2）将沿x轴方向平移（3$\sqrt{3}$±3）个单位长度与y轴相切．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．有理数a，b，c在数轴上的位置如图所示．
    （1）用“＜”连接：0，a，b，c；
    （2）化简代数式：3|c-a|+2|b-c|-3|a+b|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．在△ABC中，∠A=50°，∠B=80°，则△ABC是（　　）
    A．钝角三角形B．等腰三角形C．等边三角形D．等腰直角三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

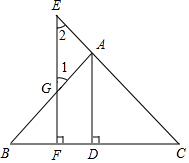    15．根据下列证明过程填空：
    已知：如 图，AD⊥BC于点D，EF⊥BC于点F，交AB于点G，交CA的延长线于点E，∠1=∠2．
    求证：AD平分∠BAC，填写证明中的空白．
    证明：
    ∵AD⊥BC，EF⊥BC  （已知），
    ∴EF∥AD   （平面内，垂直于同一条直线的两直线平行 ），
    ∴∠1=∠DAB （  两直线平行，内错角相等 ），
    ∠E=∠CAD   （两直线平行，同位角相等 ）．
    ∵∠1=∠2 （已知），
    ∴∠BAD=∠CAD，即AD平分∠BAC  （角平分线定义）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．在等腰Rt△ABC中，∠ACB=90°，AC=BC，点D是BC边上一点，BN⊥AD交AD的延长线于点N．

    （1）如图1，若CM∥BN交AD于点M．
    ①直接写出图1中所有与∠MCD相等的角：∠CAD，∠CBN；（注：所找到的相等关系可以直接用于第②小题的证明过程
    ②过点C作CG⊥BN，交BN的延长线于点G，请先在图1中画出辅助线，再回答线段AM、CG、BN有怎样的数量关系，并给予证明．
    （2）如图2，若CM∥AB交BN的延长线于点M．请证明：∠MDN+2∠BDN=180°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．有理数的计算
    （1）-14-|-7|+3-2×（-1$\frac{1}{2}$）；             
    （2）1.25×（-4）-32×（$\frac{3}{8}$-$\frac{1}{4}$-$\frac{15}{16}$）．

    查看答案和解析>>

    同步练习册答案