
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
 (2013•齐齐哈尔)如图,蜂巢的横截面由正六边形组成,且能无限无缝隙拼接,称横截面图形由全等正多边形组成,且能无限无缝隙拼接的多边形具有同形结构.
(2013•齐齐哈尔)如图,蜂巢的横截面由正六边形组成,且能无限无缝隙拼接,称横截面图形由全等正多边形组成,且能无限无缝隙拼接的多边形具有同形结构.| 2n |
| n-2 |
| 4 |
| n-2 |
| 2n |
| n-2 |
| 4 |
| n-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
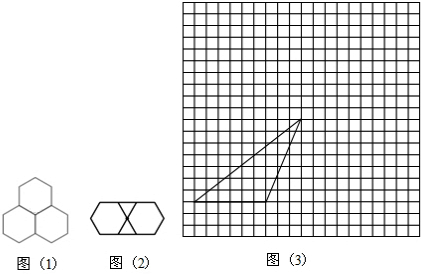
查看答案和解析>>
科目:初中数学 来源: 题型:013
选择题:
(1)在三角形的三个外角中,锐角最多只有
[ ]
(2)(n+1)边形的内角和比n边形的内角和大
[ ]
(3)若三角形三个内角的比为1:2:3,则这个三角形是
[ ]
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,蜂巢的横截面由正六边形组成,且能无限无缝隙拼接,称横截面图形由全等正多边形组成,且能无限无缝隙拼接的多边形具有同形结构.
若已知具有同形结构的正n边形的每个内角度数为α,满足:360=kα(k为正整数),多边形外角和为360°,则k关于边数n的函数是 (写出n的取值范围)

查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(黑龙江黑河、齐齐哈尔、大兴安岭卷)数学(解析版) 题型:填空题
如图,蜂巢的横截面由正六边形组成,且能无限无缝隙拼接,称横截面图形由全等正多边形组成,且能无限无缝隙拼接的多边形具有同形结构.
若已知具有同形结构的正n边形的每个内角度数为α,满足:360=kα(k为正整数),多边形外角和为360°,则k关于边数n的函数是 (写出n的取值范围)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com