Question

11．如图1，在平面直角坐标系中，直线y=-$\sqrt{3}$x+12分别与x轴、y轴交于点A，B，点C为OA中点，点P在线段OB上运动，连接CP，点O关于直线CP的对称点为点O′，射线PO′交线段AB于点E．
（1）直接写出A，B两点的坐标；
（2）①如图1，若P（0，2），求证：CO′∥AB；
    ②如图2，当点E与点O′重合时，求∠BPE的度数．
（3）当EC⊥OA时，求点P的坐标（在备用图中画出图形）．

Answer 1

分析 （1）根据x、y轴上点的坐标特点可先令y=0即可求出x的值，即A点坐标，再令x=0，求出y的值即B点坐标．
（2）①作CD⊥AB于D，根据题意证得四边形O′CDE是矩形，即可证得结论；
②根据题意求得∠2=∠OAB=60°，进一步求得∠1=30°，然后根据三角形内角和定理即可求得；
（3）根据垂直平分线的性质证得∠OCP=∠O′CP，∠CO′P=∠COP=90°，从而得∠ECP=∠EPC，即EP=EC．过E作EF⊥OB交y轴于点F，再根据勾股定理可求得FP的长，则可知OP的长，即可求得P的坐标．

解答 解：（1）∵直线y=-$\sqrt{3}$x+12分别与x轴、y轴交于点A，B，
令y=0，则0=-$\sqrt{3}$x+12，解得x=4$\sqrt{3}$，
令x=0，则y=12，
∴A（4$\sqrt{3}$，0），B（0，12）；
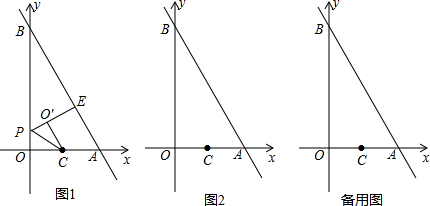
（2）①如图1，作CD⊥AB于D，
∵A（4$\sqrt{3}$，0），B（0，12），
∴OA=4$\sqrt{3}$，OB=12，
∵tan∠OAB=$\frac{OB}{OA}$=$\frac{12}{4\sqrt{3}}$=$\sqrt{3}$，
∴∠OAB=60°，
∴∠ACD=30°，
∵OP=2，OC=2$\sqrt{3}$，
∴tan∠OCP=$\frac{OP}{OC}$=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$，
∴∠OCP=30°，
∴∠OCO′=60°，
∴∠O′CD=180°-60°-30°=90°，
∵∠CO′E=90°，∠CDE=90°，
∴四边形O′CDE是矩形，
∴CO′∥AB；
②如图2，∵OC=O′C，OC=AC，
∴O′C=AC，
∵∠OAB=60°，
∴∠2=∠OAB=60°，
∵∠PO′C=∠POC=90°，
∴∠1=30°，
∵∠AOB=90°，∠OAB=60°，
∴∠PBA=30°，
∴∠BPE=180°-30°-30°=120°；
（3）如图3，过E作EF⊥OB交y轴于点F，
∵EC⊥OA，点C为OA中点，
∴EC=$\frac{1}{2}$OB=6，
∵点O、O′关于直线CP对称，
∴OP=O′P，OC=O′C．
∴△OCP≌△O′CP．
∴∠OCP=∠O′CP，∠CO′P=∠COP=90°．
∵∠OCP+∠ECP=90°，∠O′CP+∠EPC=90°，
∴∠ECP=∠EPC，
∴EP=EC=6．
∵EF=OC=2$\sqrt{3}$，
∴FP=$\sqrt{E{P}^{2}-E{F}^{2}}$=$\sqrt{36-12}$=2$\sqrt{6}$．
∵OF=CE=6，
∴OP=6-2$\sqrt{6}$．
∴P（0，6-2$\sqrt{6}$）．

点评 本题是一次函数的综合题，考查了对称的性质，解直角三角形，矩形的判定，等腰三角形的判定和性质，线段的垂直平分线的性质，熟练掌握性质定理是解题的关键．