
(2005常德)如图,AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直AB于点F,交BC于点G,连结PC,∠BAC=∠BCP,求解于列问题:
(1)求证:CP是⊙O的切线;
(2)当∠ABC=30°,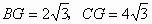 时,求以PD、PE的长为两根的一元二次方程;
时,求以PD、PE的长为两根的一元二次方程;
(3)若(1)的条件不变,当点C在劣弧AD上运动时,应再具备什么条件可使结论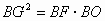 成立?试写出你的猜想,并说明理由.
成立?试写出你的猜想,并说明理由.
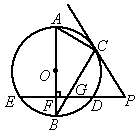
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源:2005年全国中考数学试题汇编《圆》(16)(解析版) 题型:解答题
 ;
;
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《三角形》(14)(解析版) 题型:解答题
 ,CG=
,CG= 时,求以PD、PE的长为两根的一元二次方程.
时,求以PD、PE的长为两根的一元二次方程.
查看答案和解析>>
科目:初中数学 来源:2005年湖南省常德市中考数学试卷(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2003年湖南省娄底市中考数学试卷(解析版) 题型:解答题
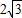 ,CG=
,CG=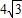 时,求以PD、PE的长为两根的一元二次方程.
时,求以PD、PE的长为两根的一元二次方程.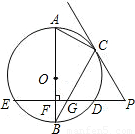
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com