
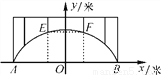
�������ҹ����ϵ��Ļ��Ų�����ͼ��ʾ��һ�������������ŵ�ʾ��ͼ����֪�����߶�Ӧ�ĺ�����ϵʽΪy����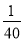 x2��10��Ϊ�������ŵİ�ȫ���ڸ��������Ͼ�ˮ��AB��Ϊ8�ĵ�E��F��Ҫ��װ��յ��ʾ�ƣ�������յ�Ƶ�ˮƽ���룮(
x2��10��Ϊ�������ŵİ�ȫ���ڸ��������Ͼ�ˮ��AB��Ϊ8�ĵ�E��F��Ҫ��װ��յ��ʾ�ƣ�������յ�Ƶ�ˮƽ���룮(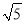 ��2.24�������ȷ��1��)
��2.24�������ȷ��1��)
 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ����������ѧУ2016-2017ѧ�����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��ijһ��ʱ������������ͼ��ʾ��������������������2����ô���������( )
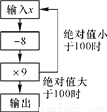
A. ��54 B. 54 C. ��558 D. 558
C ����������x=2�����������еã���2-8����9=-54�� ��x=-54�����������еã���-54-8����9=-558�� ��������Ϊ-558�� ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʦ��棩���꼶��ѧ�²ᣨ���ϣ���⣺2.2�����κ�����ͼ�������� ���ͣ���ѡ��
���ڶ��κ���y����x2��2x���������ĸ����ۣ������ĶԳ�����ֱ��x��1������y1����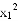 ��2x1��y2����
��2x1��y2����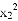 ��2x2����x2��x1ʱ����y2��y1��������ͼ����x�������������(0��0)��(2��0)���ܵ�0��x��2ʱ��y��0.������ȷ���۵ĸ���Ϊ(����)
��2x2����x2��x1ʱ����y2��y1��������ͼ����x�������������(0��0)��(2��0)���ܵ�0��x��2ʱ��y��0.������ȷ���۵ĸ���Ϊ(����)
A. 1 B. 2 C. 3 D. 4
C ����������������������䷽��������κ����Գ��ᣬ�����ͼ����x�ύ�����꣬������϶��κ������ʵó��𰸣� y=��x2+2x=����x��1��2+1���ʢ����ĶԳ�����ֱ��x=1����ȷ�� �ڡ�ֱ��x=1���Բ��������Բ�һ���� ����y1=��x12+2x1��y2=��x22+2x2����x2��x1ʱ����y2��y1��y2��y1������ �۵�y=0����x����x+2��=0����ã�x1=0��x2=2�� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʦ��棩���꼶��ѧ�²ᣨ���ϣ���⣺2.2�����κ�����ͼ�������� ���ͣ���ѡ��
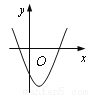
��֪���κ���y��a(x��1)2��c��ͼ����ͼ��ʾ����һ�κ���y��ax��c�Ĵ���ͼ������ǣ� ��
A. 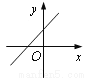 B.
B. 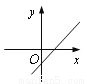 C.
C. 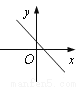 D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʦ��棩���꼶��ѧ�²ᣨ���ϣ���⣺2.2�����κ�����ͼ�������� ���ͣ������
��֪����y����(x��1)2ͼ��������A(2��y1)��B(a��y2)������a��2����y1��y2�Ĵ�С��ϵ��y1_____y2.(���������������)
�� ��������������������ݺ�������ʽ�����ж������߶Գ�����x=1,�������£����Ե�x>1ʱ��y��x���������С��a>2,����y1>y2�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʦ��棩���꼶��ѧ�²ᣨ���ϣ���⣺2.2�����κ�����ͼ�������� ���ͣ���ѡ��
��֪������y=x2+1�����������ʣ���������������һ�㵽����F��0��2���ľ����뵽x��ľ���ʼ����ȣ���ͼ����M������Ϊ��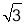 ��3����P��������y=
��3����P��������y=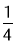 x2+1��һ�����㣬���PMF�ܳ�����Сֵ�ǣ� ��
x2+1��һ�����㣬���PMF�ܳ�����Сֵ�ǣ� ��
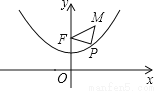
A��3 B��4 C��5 D��6
C�� �������� �������������M��ME��x���ڵ�E����������y=x2+1�ڵ�P����ʱ��PMF�ܳ���Сֵ�� ��F��0��2����M�� ��3���� ��ME=3��FM==2�� ���PMF�ܳ�����Сֵ=ME+FM=3+2=5�� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʦ��棩���꼶��ѧ�²ᣨ���ϣ���⣺2.2�����κ�����ͼ�������� ���ͣ���ѡ��
��ƽ��ֱ������ϵ�У���������y��x2��4����ƽ��2����λ���ȣ��õ��������߱���ʽΪ( )
A. y��(x��2)2 B. y��x2��2
C. y��(x��2)2 D. y��x2��2
D ����������������������ߵĶԳ�����y�ᣬ������y���ϣ���0��-4������ƽ��������λ�������Ϊ��0��-2�������������߱���ʽ��y��x2��2����ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʦ��棩���꼶��ѧ�²ᣨ���ϣ���⣺2.2�����κ�����ͼ�������� ���ͣ������
��ͬһƽ��ֱ������ϵ�У��������к�����ͼ��
(1)y��2x2��(2)y��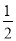 x2.
x2.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����й���ѧУ2018����꼶��ѧ�ڵڶ��ζο������У�������ѧ�Ծ� ���ͣ������
��ij�ξۻ��ϣ�ÿ���˶�����һ���֣������˹�����36�Σ��μӾۻ����________�ˣ�
9 �������������������μ���ξۻ����x�ˣ�ÿ���˶��������������һ�Σ���ÿ�������֣�x��1���Σ��������κ����˵�����ֻ��һ�Σ��������x��x��1���Σ� ���������з��̵ã� x��x��1����36�� ���x1��9��x2����8���������⣬��ȥ���� �𣺲μ���ξۻ����9�ˣ� �ʴ�Ϊ9���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com