练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    菱形的面积为，一条对角线长为6cm，则另一条对角线长为________cm，菱形高为________cm．

    答案：8,4.8
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    某中学有一块长为a米，宽为b米的矩形场地，计划在该场地上修筑宽都为2米的两条互相垂直的道路，余下的四块矩形小场地建成草坪．
    （1）如图，请分别写出每条道路的面积（用含a或含b的代数式表示）；
    （2）已知a：b=2：1，并且四块草坪的面积之和为312米2，试求原来矩形场地的长与宽各为多少米？
    （3）在（2）的条件下，为进一步美化校园，根据实际情况，学校决定对整个矩形场地作如下设计（要求同时符合下述两个条件）：
    条件①：在每块草坪上各修建一个面积尽可能大的菱形花圃（花圃各边必须分别与所在草坪的对角线平行），并且其中有两个花圃的面积之差为13米2；
    条件②：整个矩形场地（包括道路、草坪、花圃）为轴对称图形．
    请你画出符合上述设计方案的一种草图（不必说明画法与根据），并求出每个菱形花圃的面积．精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若菱形的两条对角线的比为3：4，且周长为20cm，则它的一组对边的距离等于
     
    cm，它的面积等于
     
    cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，矩形铁片ABCD中，AD=8，AB=4； 为了要让铁片能穿过直径为3.8的圆孔，需对铁片进行处理 （规定铁片与圆孔有接触时铁片不能穿过圆孔）．
    （1）直接写出矩形铁片ABCD的面积
    32
    32
    ；
    （2）如图2，M、N、P、Q分别是AD、AB、BC、CD的中点，将矩形铁片的四个角去掉．
    ①证明四边形MNPQ是菱形；
    ②请你通过计算说明四边形铁片MNPQ能穿过圆孔．
    （3）如图3，过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F（不与端点重合），沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片．当BE=DF=1时，判断直角梯形铁片EBAF能否穿过圆孔，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2012届福建省永春县九年级上学期期末数学试卷（带解析） 题型：解答题

    如图1, 矩形铁片ABCD中，AD="8," AB="4;" 为了要让铁片能穿过直径为3.8的圆孔, 需对铁片进行处理 (规定铁片与圆孔有接触时铁片不能穿过圆孔).
    (1)直接写出矩形铁片ABCD的面积           ；
    (2)如图2, M、N、P、Q分别是AD、AB、BC、CD的中点,将矩形铁片的四个角去掉.
    ①证明四边形MNPQ是菱形；
    ②请你通过计算说明四边形铁片MNPQ能穿过圆孔.
    (3)如图3, 过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合), 沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片.当BE=DF=1时,判断直角梯形铁片EBAF能否穿过圆孔, 并说明理由.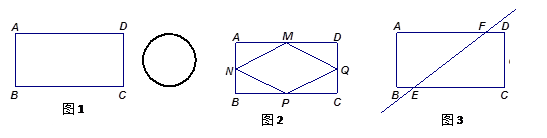

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年福建省永春县九年级上学期期末数学试卷（解析版） 题型：解答题

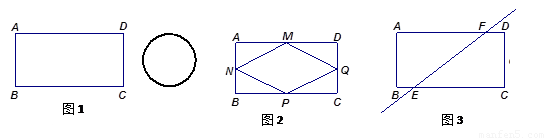
    如图1, 矩形铁片ABCD中，AD=8, AB=4; 为了要让铁片能穿过直径为3.8的圆孔, 需对铁片进行处理 (规定铁片与圆孔有接触时铁片不能穿过圆孔).

    (1)直接写出矩形铁片ABCD的面积            ；

    (2)如图2, M、N、P、Q分别是AD、AB、BC、CD的中点,将矩形铁片的四个角去掉.

    ① 证明四边形MNPQ是菱形；

    ②请你通过计算说明四边形铁片MNPQ能穿过圆孔.

    (3)如图3, 过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合), 沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片.当BE=DF=1时,判断直角梯形铁片EBAF能否穿过圆孔, 并说明理由.

     

    查看答案和解析>>

    同步练习册答案