
下列算式结果为-2的是( )
A. 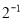 B. (-2)0 C.
B. (-2)0 C. 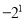 D.
D. 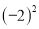
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源:2017-2018学年河南省南阳市镇平县七年级(上)12月月考数学试 题型:单选题
以下四个选项表示某天四个城市的平均气温,其中平均气温最低的是( )
A. -3℃ B. 15℃ C. -10℃ D. -1℃
C 【解析】试题分析:因为-10℃<-3℃<-1℃<15℃,所以平均气温最低的是-10℃,故选:C.查看答案和解析>>
科目:初中数学 来源:人教版八年级下册 第十六章 《二次根式》复习测试 题型:单选题
若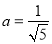 ,
, 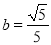 ,则a、b两数的关系是( )
,则a、b两数的关系是( )
A. 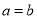 B.
B. 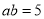 C.
C. 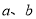 互为相反数 D.
互为相反数 D. 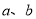 互为倒数
互为倒数
查看答案和解析>>
科目:初中数学 来源:广东省汕头市龙湖区2017-2018学年八年级上学期期末质量检测数学试卷 题型:解答题
下面是小颖化简的过程,仔细阅读后解答所提出的问题.
【解析】
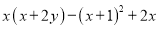
=(x2+2xy)﹣(x2+1)+2x 第一步
=x2+2xy﹣x2﹣1+2x 第二步
=2xy+2x -1 第三步
(1)小颖的化简过程从第 步开始出现错误;
(2)对此整式进行化简.
(1)一;(2)2xy﹣1. 【解析】试题分析:(1)第一步出现错误,利用完全平方公式进行展开时落项了; (2)先利用单项式乘多项式、完全平方公式进行展开,然后再进行合并同类项即可得. 试题解析:(1)第一步出错; (2)原式=(x2+2xy)﹣(x2+2x+1)+2x=x2+2xy﹣x2﹣2x﹣1+2x=2xy﹣1.查看答案和解析>>
科目:初中数学 来源:广东省汕头市龙湖区2017-2018学年八年级上学期期末质量检测数学试卷 题型:单选题
将图(甲)中阴影部分的小长方形变换到图(乙)位置,根据两个图形的面积关系得到的数学公式是( )

A.(a+b)2=a2+2ab+b2
B.(a﹣b)2=a2﹣2ab+b2
C.a2﹣b2=(a+b)(a﹣b)
D.(a+2b)(a﹣b)=a2+ab﹣2b2
C 【解析】 试题分析:根据阴影部分的面积相等的法则进行计算.查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学 第一章 三角形的证明 单元检测卷 题型:解答题
如图,(1)P是等腰三角形A BC底边BC上的一人动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R。请观察AR与AQ,它们有何关系?并证明你的猜想。

(2)如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论还成立吗?请你在图15(2)中完成图 形,并给予证明。
直角三角形的角度运算规律;AR=AQ 【解析】试题分析:(1)由已知条件,根据等腰三角形两底角相等及三角形两直角互余的性质不难推出∠PRC与∠AQR的关系; (2)由已知条件,根据等腰三角形两底角相等及三角形两直角互余的性质不难推出∠BQP与∠PRC的关系. 【解析】 (1)AR=AQ,理由如下: ∵AB=AC, ∴∠B=∠C. ∵RP⊥BC, ∴∠B+...查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学 第一章 三角形的证明 单元检测卷 题型:填空题
直角三角形是特殊的三角形,所以不仅可以应用一般三角形判定全等的方法,还有直角三角形特殊的判定方法,即 ________公理.
HL 【解析】直角三角形是特殊的三角形,所以不仅可以应用一般三角形判定全等的方法,还有直角三角形特殊的判定方法,即HL公理, 故答案为:HL.查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学 第一章 三角形的证明 单元检测卷 题型:单选题
已知等腰三角形的一个内角为70°,则另两个内角的度数是( )
A. 55°,55° B. 70°,40°
C. 55°,55°或70°,40° D. 以上都不对
C 【解析】试题分析:分别把70°看做等腰三角形的顶角和底角,分两种情况考虑,利用三角形内角和是180度计算即可. 【解析】 当70°为顶角时,另外两个角是底角,它们的度数是相等的,为(180°﹣70°)÷2=55°, 当70°为底角时,另外一个底角也是70°,顶角是180°﹣140°=40°. 故选C.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学 第九章 不等式与不等式组 单元检测卷 题型:单选题
如果不等式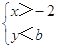 无解,则b的取值范围是( )
无解,则b的取值范围是( )
A. b>-2 B. b<-2 C. b≥-2 D. b≤-2
D 【解析】试题分析:不等式组无解就是两个不等式的解集没有公共部分,可利用数轴进行求解. 【解析】 x>﹣2在数轴上表示点﹣2右边的部分,x<b表示点b左边的部分. 当点b在﹣2这点或这点的左边时,两个不等式没有公共部分,即不等式组无解, 则b≤﹣2. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com