
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:解答题
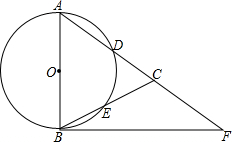 如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且BF是⊙O的切线.
如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且BF是⊙O的切线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 13 | 16 | 17 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
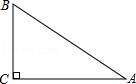 如图,已知斜坡AB的水平宽度是8米,斜坡AB的坡度为1:2,则斜坡AB的长为( )
如图,已知斜坡AB的水平宽度是8米,斜坡AB的坡度为1:2,则斜坡AB的长为( )| A. | 4$\sqrt{3}$ | B. | 4$\sqrt{5}$ | C. | 18 | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
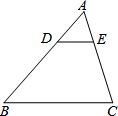 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD=1,BD=2,则$\frac{DE}{BC}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲骑车到乙家研讨数学问题,中途因等候红灯停止了一分钟,之后又骑行了1.2千米到达了乙家.若甲骑行的速度始终不变,从出发开始计时,剩余的路程S(单位:千米)与时间t(单位:分钟)的函数关系的图象如图所示,则图中a等于( )
甲骑车到乙家研讨数学问题,中途因等候红灯停止了一分钟,之后又骑行了1.2千米到达了乙家.若甲骑行的速度始终不变,从出发开始计时,剩余的路程S(单位:千米)与时间t(单位:分钟)的函数关系的图象如图所示,则图中a等于( )| A. | 1.2 | B. | 2 | C. | 2.4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
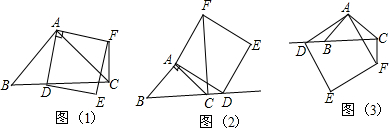
 如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com