
用加减法解方程组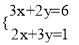 时,要使方程中同一个未知数的系数相等或互为相反数,必须适当变形,以下四种变形正确的是( )
时,要使方程中同一个未知数的系数相等或互为相反数,必须适当变形,以下四种变形正确的是( )
①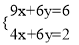 ②
②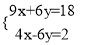 ③
③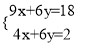 ④
④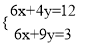
A. ①② B. ②③ C. ③④ D. ①④
C 【解析】试题分析: 把y的系数变为相等时,①×3,②×2得, , 把x的系数变为相等时,①×2,②×3得, , 所以③④正确. 故选C. 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(2)测试 题型:填空题
与抛物线y=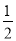 x2的形状和开口方向相同,顶点为(3,1)的二次函数解析式为______.
x2的形状和开口方向相同,顶点为(3,1)的二次函数解析式为______.
查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
如图所示, AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=_____.
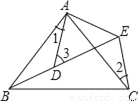
查看答案和解析>>
科目:初中数学 来源:重庆市华东师大版2016-2017学年七年级下学期期中考试数学试卷 题型:填空题
我们知道,完全平方式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,如:(2m+n)(m+n)=2m2+3mn+n2,就可以用图①的面积表示,观察图②,请你写出三个代数式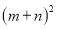 ,
,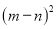 ,
, 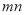 之间的等量关系是_________________________。
之间的等量关系是_________________________。
查看答案和解析>>
科目:初中数学 来源:重庆市华东师大版2016-2017学年七年级下学期期中考试数学试卷 题型:单选题
如图,设他们中有x个成人,y个儿童.根据图中的对话可得方程组( )
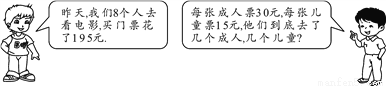
A. 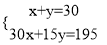 B.
B. 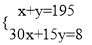
C. 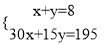 D.
D. 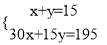
查看答案和解析>>
科目:初中数学 来源:重庆市华东师大版2016-2017学年七年级下学期期中考试数学试卷 题型:单选题
下列是二元一次方程的是( )
A. 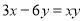 B.
B. 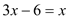 C.
C. 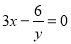 D.
D. 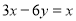
查看答案和解析>>
科目:初中数学 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:填空题
M为矩形ABCD的BC上一点,DN⊥AM于N,AB=3,BC=7,AM=5,则DN=______.
【解析】∵四边形ABCD是矩形,∴AD=BC=7,∠B=90°,AD//BC, ∴∠AMB=∠DAN, ∵∠AND=90°=∠B, ∴△ADN∽△MAB, ∴,即 ,∴DN= , 故答案为: .查看答案和解析>>
科目:初中数学 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:单选题
已知矩形ABCD的AB=2BC,在CD上取点E,使AE=EB,那么∠EBC等于( ).
A. 60° B. 45° C. 30° D. 15°
B 【解析】作EM⊥AB于M , ∵AE=BE, ∴M为AB中点 , ∵AB=2BC, ∴AM=BM=EM , ∴∠MBE=∠MEB=45°, ∴∠EBC=45°, 故选B.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 25.1.1随机事件 测试 题型:填空题
为了了解参加某运动会的2000名运动员的年龄情况,从中抽查了100名运动员的年龄,“某运动员被抽到”这一事件是____事件,抽到的可能性为____.
随机 【解析】根据随机事件的性质可得,因为为了了解参加某运动会的2000名运动员的年龄情况,从中抽查了100名运动员的年龄,所以在2000名运动员抽查100名运动员,所以这一事件为随机事件,且抽到的可能性为100÷2000=. 故答案为:随机, .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com