解:(1)∵B(

,1),
∴AB=OC=1,
OB=

=2,
根据翻折的性质,OE=OC=1,
①AB=BE时,则OE+BE=OB=2,
所以,点O、E、B三点共线,且点E是OB的中点,
∵O(0,0),B(

,1),
∴点E的坐标为(

,

),
②AE=BE时,根据等腰三角形三线合一的性质可得点E在AB的垂直平分线上,
所以,点E的纵坐标为

,
过点E作EF⊥OA于点F,则OF=

=

=

,
所以,点E的坐标为(

,

),
③AE=AB时,∵OE=AE=1,
∴点E在OA的垂直平分线上,
∴OF=

OA=

,
∴EF=

=
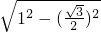
=

,
∴点E的坐标为(

,

),
综上所述,点E的坐标为(

,

);
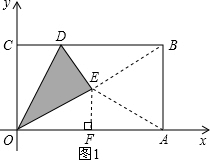
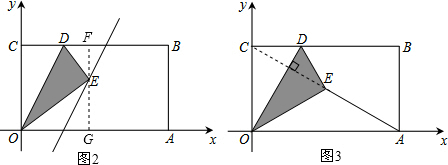
(2)如图2,过点E作OC的平行线交BE于F,交OA于G,可得EF⊥BC,EG⊥OA,
∵点E在一次函数y=2x-1的图象上,
∴设点E坐标为(a,2a-1),
在Rt△OEG中,OE
2=EG
2+OG
2,
即1
2=(2a-1)
2+a
2,
整理得,5a
2-4a=0,
解得a
1=0(舍去),a
2=

,
∴OG=

,EG=2×

-1=

,
∴EF=FG-EG=1-

=

,
根据翻折,∠DEO=∠OCD=90°,
∴∠DEF+∠OEG=180°-90°=90°,
∵∠EOG+∠OEG=90°,
∴∠EOG=∠DEF,
又∵∠EDF=∠OGE=90°,
∴△OGE∽△EFD,
∴
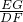
=

,
即
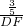
=
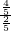
,
解得DF=

,
∴CD=CF-DF=OG-DF=

-

=

,
∴点D的坐标为(

,1);
(3)如图3,连接CE,根据翻折对称性,CE⊥OD,
∵AE⊥OD,
∴A、E、C三点共线,
∵∠OAE+∠OCE=90°,∠COD+∠OCE=90°,
∴∠OAE=∠COD,
矩形OABC的对角线AC=OB=2,
∵cos∠OAE=

=

,
cos∠COD=

=
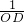
,
∴
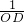
=

,
解得OD=

,
∵OD是Rt△OCD与Rt△ODE的斜边,
∴点O、C、D、E四点共圆,且OD是外接圆的直径,
∴△CDE的外接圆的半径为:

OD=

×

=

.
分析:(1)分①AB=BE时,根据勾股定理求出OB=2,从而判断出O、E、B三点共线,从而确定点E为矩形OABC的中心,然后根据点B的坐标写出即可;
②AE=BE,然后根据等腰三角形三线合一的性质可以判定点E的纵坐标为

,再根据翻折的性质可得OE=OC=1,过点E作EF⊥OA于点F,根据勾股定理求出OF的长度,即可得到点E的坐标;
③AE=AB时,可以得到AE=OE,根据等腰三角形三线合一的性质可得点E在OA的垂直平分线上,然后利用勾股定理求出点E到OA的距离EF的长度,即可得解;
(2)过点E作OC的平行线交BE于F,交OA于G,可得EF⊥BC,EG⊥OA,然后根据直线解析式设出点E的坐标,利用勾股定理列式求解得到点E的坐标,然后证明△OGE和△EFD相似,根据相似三角形对应边成比例列式求出DF的长度,然后求出CD的长度,即可得到点D的坐标;
(3)连接CE,根据翻折的对称性可得CE⊥OD,再根据过一点有且只有一条直线与已知直线垂直可得A、E、C三点共线,再根据直角三角形两锐角互余求出∠OAE=∠COD,再根据勾股定理求出AC的长度,然后利用∠OAE与∠COD的余弦值相等列式求解即可得到OD的长度,再证明△CDE的外接圆是以OD为直径的圆,从而得解.
点评:本题是对一次函数的综合考查,主要利用了翻折变换的性质,等腰三角形的性质,勾股定理,以及相似三角形的判定与性质,(1)要根据等腰三角形的腰进行讨论,(2)先根据直线解析式求出点E的坐标是解题的关键,(3)判断出点A、E、C三点共线是解题的关键.

 ,1),在BC边上选取适当的点D,将△OCD沿OD翻折,点C落在点E处,得到△OED.
,1),在BC边上选取适当的点D,将△OCD沿OD翻折,点C落在点E处,得到△OED.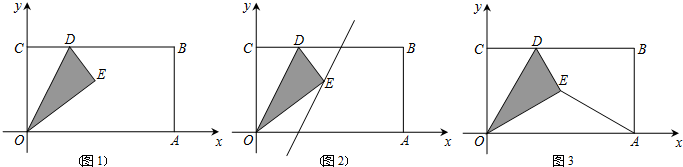
 解:(1)∵B(
解:(1)∵B( ,1),
,1), =2,
=2, ,1),
,1), ,
, ),
), ,
, =
= =
= ,
, ,
, ),
), OA=
OA= ,
, =
=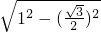 =
= ,
, ,
, ),
), ,
, );
); ,
, ,EG=2×
,EG=2× -1=
-1= ,
, =
= ,
,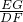 =
= ,
,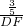 =
=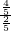 ,
, ,
,
 -
- =
= ,
, ,1);
,1); =
= ,
, =
=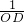 ,
,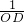 =
= ,
, ,
, OD=
OD= ×
× =
= .
. ,再根据翻折的性质可得OE=OC=1,过点E作EF⊥OA于点F,根据勾股定理求出OF的长度,即可得到点E的坐标;
,再根据翻折的性质可得OE=OC=1,过点E作EF⊥OA于点F,根据勾股定理求出OF的长度,即可得到点E的坐标;

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案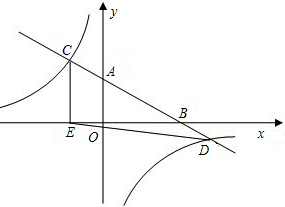 反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=
反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=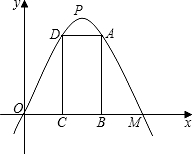 M=4,矩形ABCD的边BC在线段OM上,点A、D在抛物线上.
M=4,矩形ABCD的边BC在线段OM上,点A、D在抛物线上. ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.