解:(1)①∵B(3,0),C(0,2),
∴将点C向下平移2个单位,再向右平移3个单位与点B重合.
故答案为2,3; (每空,共2分)
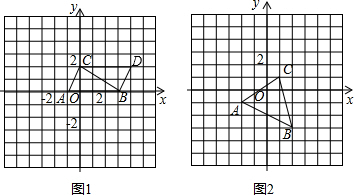
②点D位置如图所示.
证明:由图可知AB∥CD,AB=CD,
∴四边形ABCD是平行四边形;
(2)以△ABC的两条边为边,第三边为对角线的平行四边形有几个共有3个.
①以AB、AC为边可作一平行四边形,第四个顶点的坐标为(5,-1);
②以CA、CB为边可作一平行四边形,第四个顶点的坐标为(-1,-5);
③以BA、BC为边也可作一平行四边形,则第四顶点的坐标为(-3,3).
分析:(1)根据平移的规律:上加下减,左加右减即可得出将点C向下平移2个单位,再向右平移3个单位与点B重合;
(2)根据平移的规律:上加下减,左加右减得出将点D的坐标为(4,2),然后根据一组对边平行且相等的四边形是平行四边形证出四边形ABDC是平行四边形;
(3)分别以AB,BC,AC为平行四边形的对角线,考虑第四个顶点D的坐标,有三种可能结果.
点评:本题主要考查坐标与图形变化-平移,平行四边形的判定,并与坐标相结合,学生需要熟练求解此类问题.


 ②点D位置如图所示.
②点D位置如图所示.

 如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF.
如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF.