
 时,求AD的长.
时,求AD的长.
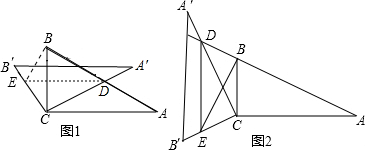 解:(1)在Rt△ABC中,∵∠A=30°,
解:(1)在Rt△ABC中,∵∠A=30°,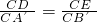 .
.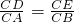 ,
,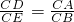 .
.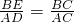 .
. =
=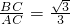 .
. (0<x<2)
(0<x<2)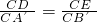 ,
,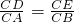 ,
,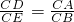 ,
, .
.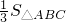 时,
时,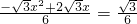 .
.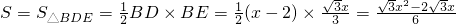 .
.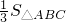 时,
时,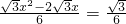 .
.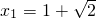 ,
,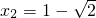 (负值,舍去).
(负值,舍去).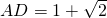 .
.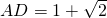 .
.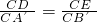 、及由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE由此证明△CAD∽△CBE;根据相似三角形的对应边成比例、直角三角形的性质及∠A=30°求得
、及由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE由此证明△CAD∽△CBE;根据相似三角形的对应边成比例、直角三角形的性质及∠A=30°求得 (0<x<2);
(0<x<2);

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
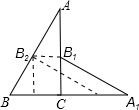 如图,直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板绕顶点C按顺时针方向旋转90°至△A1B1C的位置,沿CB向左平移使B1点落在△ABC的斜边AB上,点B1平移到点B2,则点B由B?B1?B2运动的路程是( )
如图,直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板绕顶点C按顺时针方向旋转90°至△A1B1C的位置,沿CB向左平移使B1点落在△ABC的斜边AB上,点B1平移到点B2,则点B由B?B1?B2运动的路程是( )A、(3π+3-
| ||||
B、(3π-3+
| ||||
C、(
| ||||
D、(
|
查看答案和解析>>
科目:初中数学 来源: 题型:
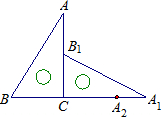 如图直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板ABC绕着直角顶点C顺时针方向旋转90°至△A1B1C1的位置,再沿CB向左平移使点B1落在△ABC的斜边AB上,点A1平移到点A2的位置,则点A?A1?A2运动的路径长度是
如图直角三角板ABC中,∠A=30°,BC=3cm,将直角三角板ABC绕着直角顶点C顺时针方向旋转90°至△A1B1C1的位置,再沿CB向左平移使点B1落在△ABC的斜边AB上,点A1平移到点A2的位置,则点A?A1?A2运动的路径长度是查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com