
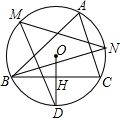
 如图,在⊙0中,点D、M、N分别为弧BC、弧AB、弧AC的中点,OH=DH,下列结论:①∠A=60°;
如图,在⊙0中,点D、M、N分别为弧BC、弧AB、弧AC的中点,OH=DH,下列结论:①∠A=60°;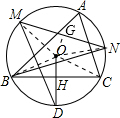 解:连接OB,OC,
解:连接OB,OC, OD=
OD= OB,
OB, ,
, ∠BOC=60°,故选项①正确;
∠BOC=60°,故选项①正确;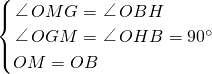 ,
,

科目:初中数学 来源: 题型:
 (2007•上海模拟)已知:如图,在△ABC中,点A的坐标为(-3,4),点B的坐标为(-1,-4),点C的坐标为(3,-1).
(2007•上海模拟)已知:如图,在△ABC中,点A的坐标为(-3,4),点B的坐标为(-1,-4),点C的坐标为(3,-1).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•南宁模拟)如图,在△ABC中,点D在AC上,DA=DB,∠C=∠DBC,以AB为直径的⊙O交AC于点E,F是⊙O上的点,且AF=BF.
(2012•南宁模拟)如图,在△ABC中,点D在AC上,DA=DB,∠C=∠DBC,以AB为直径的⊙O交AC于点E,F是⊙O上的点,且AF=BF.| 3 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2004•静安区二模)如图,在△ABC中,点D、G分别在BC、AB边上,AD与CG相交H,如果DA=DB,GB=GC,AD平分∠BAC,那么下列三角形中不与△ABC相似的是( )
(2004•静安区二模)如图,在△ABC中,点D、G分别在BC、AB边上,AD与CG相交H,如果DA=DB,GB=GC,AD平分∠BAC,那么下列三角形中不与△ABC相似的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com