
计算: 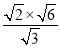 +(
+(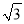 ﹣2)2﹣
﹣2)2﹣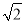 (
(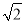 ﹣
﹣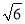 )
)
科目:初中数学 来源:北京市2016-2017学年七年级(下)期中数学试卷 题型:填空题
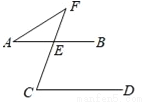
如图,AB∥CD,∠A=34°,∠C=70°,则∠F=______°.
查看答案和解析>>
科目:初中数学 来源:山东省东营市河口区2017-2018学年度第一学期期末考试七年级数学试卷 题型:解答题
为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担,若国家财政拨付资金不超过11800万元,地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校改扩建资金分别为每所300万元和500万元,请问共有哪几种改扩建方案?
(1)1200万元或1800万元;(2)有三种方案. 【解析】试题分析:(1)可根据“改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元”,列出方程组求出答案; (2)要根据“国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元”来列出不等式组,判断出不同的改造方案. 试题解析:(1)设改扩建一所A类和一...查看答案和解析>>
科目:初中数学 来源:山东省东营市河口区2017-2018学年度第一学期期末考试七年级数学试卷 题型:单选题
为丰富学生课外活动,某校积极开展社团活动,学生可根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球C:足球;D:羽毛球,E:乒乓球.李老师对某年级同学选择体育社团情况进行调查统计,制成了两幅不完整的统计图(如图),则以下结论不正确的是( )
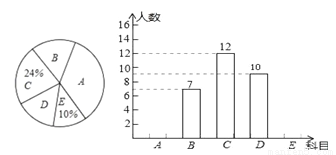
A. 选科目E的有5人
B. 选科目D的扇形圆心角是72°
C. 选科目A的人数占体育社团人数的一半
D. 选科目B的扇形圆心角比选科目D的扇形圆心角的度数少21.6°
C 【解析】试题分析:A选项先求出调查的学生人数,再求选科目E的人数来判定, B选项利用×360°判定即可, C选项中求出B,C,D的人数即可判定, D选项利用选科目B的人数减选科目D,再除以总人数乘360°求解即可判定. 【解析】 调查的学生人数为:12÷24%=50(人),选科目E的人数为:50×10%=5(人),故A选项正确, 选科目D的扇形圆心角是×3...查看答案和解析>>
科目:初中数学 来源:山东省东营市河口区2017-2018学年度第一学期期末考试七年级数学试卷 题型:单选题
在下列各数中0.333…,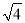 ,
, 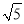 ,
, 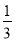 ,2π,3.14,2.0101010…(相邻两个1之间有1个0)是无理数的有( )
,2π,3.14,2.0101010…(相邻两个1之间有1个0)是无理数的有( )
A. 2个 B. 3个 C. 4个 D. 6个
A 【解析】根据无理数的概念,无限不循环小数,可知, 2π是无理数,共有2个. 故选:A.查看答案和解析>>
科目:初中数学 来源:广东省实验学校2017-2018学年八年级(上)期中数学试卷 题型:填空题
如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是_____.
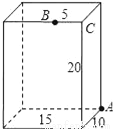
查看答案和解析>>
科目:初中数学 来源:广东省实验学校2017-2018学年八年级(上)期中数学试卷 题型:单选题
如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要( )米.
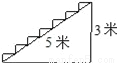
A. 5 B. 7 C. 8 D. 12
B 【解析】根据勾股定理求得楼梯的水平宽度==4,然后由地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,地毯的长度至少是3+4=7米. 故选:B.查看答案和解析>>
科目:初中数学 来源:江西省赣州市2017-2018学年七年级(上)期中数学试卷 题型:解答题
有理数a,b,c在数轴上的位置如图所示,且|a|=|c|.
(1)若|a+c|+|b|=2,求b的值;
(2)用“>”从大到小把a,b,﹣b,c连接起来.
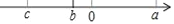
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市蓬溪县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
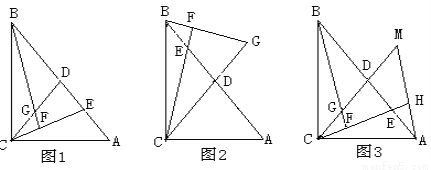
已知:在△ABC中,AC=BC, 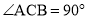 ,过点C作CD⊥AB于点D,点E是AB边上一动点(不同于点A、B),连接CE,过点B作CE的垂线交直线CE于点F,交直线CD于点G(如图1).
,过点C作CD⊥AB于点D,点E是AB边上一动点(不同于点A、B),连接CE,过点B作CE的垂线交直线CE于点F,交直线CD于点G(如图1).
(1)求证:BG=CE;
(2)若点E运动到线段BD上时(如图2),试猜想BG、CE的数量关系是否发生变化?请直接写出你的结论;
(3)过点A作AH垂直于直线CE垂足为点H并交CD的延长线于点M(如图3),找出图中与BE相等的线段,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com