
(1)计算:cos30°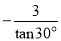 ;
;
(2)解方程: x(x+3)=2x+1.
(1)(2), . 【解析】试题分析: 把三角函数的特殊值代入运算即可. 用公式法解一元二次方程. 试题解析: (1)原式. (2)方程整理得: , . 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
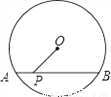
如图,已知AB是⊙O的弦,P是AB上一点,AB=10,PA=4,OP=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:单选题
下列函数中,二次函数是
A. y=-4x+5 B. y=x(2x-3) C. 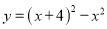 D.
D. 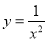
查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:单选题
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中正确的是( )
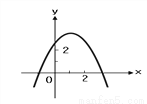
A. abc>0 B. a+b+c>0 C. c<0 D. b<0
B 【解析】【解析】 抛物线开口向下,则a<0,抛物线的对称轴在y轴的右侧,则b<0,抛物线与x轴的交点在x轴上方,则c>0,所以A选项,C选项、D选项都错误; 由于x=1时,y>0,即a+b+c>0,所以B选项正确. 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:解答题
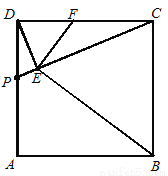
如图,正方形ABCD中,点P是AD上的一动点(与点D、点A不重合),DE⊥CP,垂足为E,EF⊥BE与DC交于点F.
(1)求证:△DEF∽△CEB;
(2)当点P运动到DA的中点时,求证:点F为DC的中点.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:填空题
若二次根式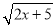 在实数范围内有意义,则x的取值范围是___________.
在实数范围内有意义,则x的取值范围是___________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:单选题
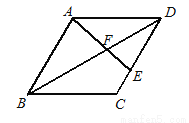
如图,□ABCD中,点E在CD上,AE交BD于点F,若DE =2CE,则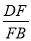 等于( )
等于( )
A. 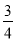 B.
B. 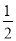 C.
C. 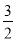 D.
D. 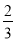
查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年度七年级第一学期人教版数学期末自测试卷(二) 题型:填空题
若5xm+1y5与3x2y2n+1是同类项,则m=________,n=________.
1 2 【解析】根据同类项的定义,得出关于m,n的方程,求出m,n的值. 【解析】 ∵单项式5xm+1y5与3x2y2n+1是同类项, ∴m+1=2,m=1,2n+1=5, n=2, 故答案为:1,2. “点睛”本题考查了同类项的知识,解答本题的关键是掌握同类项定义中的两个“相同”:相同字母的指数相同.查看答案和解析>>
科目:初中数学 来源:辽宁省2018届九年级(上)期末模拟数学试卷 题型:解答题
已知a、b、c为△ABC的三边长,化简: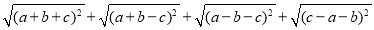 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com