练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    一个两位数，十位数字为a，个位数字为b，这个两位数可以表示为_____．

    10a+b 【解析】两位数=10×十位数字+个位数字， 所以这个两位数可以表示为：10a+b， 故答案为：10a+b.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：贵州省2017-2018学年八年级（上）期中数学试卷 题型：单选题

    若等腰三角形的两边长分别是3和6，则这个三角形的周长是（ ）

    A. 12 B. 15 C. 12或15 D. 9

    B 【解析】试题分析：根据题意，要分情况讨论：①、3是腰；②、3是底．必须符合三角形三边的关系，任意两边之和大于第三边． 【解析】 ①若3是腰，则另一腰也是3，底是6，但是3+3=6，∴不构成三角形，舍去． ②若3是底，则腰是6，6． 3+6＞6，符合条件．成立． ∴C=3+6+6=15． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：北京市2016-2017学年七年级（下）期中数学试卷 题型：解答题

    （1）；

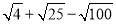    （2）．

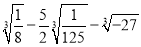    （1）－3；（2）3． 【解析】试题分析：（1）直接利用算术平方根定义分析得出答案； （2）直接利用立方根的性质化简得出答案． 【解析】 （1） =2+5﹣10 =﹣3； （2） =﹣×+3 =3．

    查看答案和解析>>

    科目：初中数学 来源：北京市2016-2017学年七年级（下）期中数学试卷 题型：单选题

    以下列各组线段为边，能组成三角形的是(　　)

    A. 2cm，3cm，5cm B. 5cm，6cm，10cm

    C. 1cm，1cm，3cm D. 3cm，4cm，9cm

    B 【解析】试题分析：A项，2+3=5，不构成三角形；B项，5+6>10，可构成三角形；C项1+1<3，不构成三角形；D项，3+4<8，不构成三角形，只有B项符合题意.

    查看答案和解析>>

    科目：初中数学 来源：浙江省平阳县2017-2018学年第一学期第二次阶段检测（期末）七年级数学试卷 题型：填空题

    如果代数式2y2+3y+5的值是6，求代数式4y2+6y-3的值是 ．

    -1． 【解析】 试题解析：∵代数式2y2+3y+5的值是6， ∴2y2+3y+5=6． ∴2y2+3y=1． ∴4y2+6y-3=2（2y2+3y）-3=2-3=-1．

    查看答案和解析>>

    科目：初中数学 来源：浙江省平阳县2017-2018学年第一学期第二次阶段检测（期末）七年级数学试卷 题型：单选题

    一家商店将某种服装按成本价提高40%标价，又以8折优惠卖出，结果每件服装仍可获利15元，则这种服装每件的成本价是（　　）

    A. 140元 B. 135元 C. 125元 D. 120元

    C 【解析】设这种服装每件的成本价为x元，根据标价-成本=利润，可得：80%×（1+40%）x﹣x=15，解得：x=125．这种服装每件的成本为125元． 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：浙江省平阳县2017-2018学年第一学期第二次阶段检测（期末）七年级数学试卷 题型：单选题

    下列一组数：﹣8，0，﹣32，﹣（﹣5.7），其中负数的个数有（　　）

    A. 1个 B. 2个 C. 3个 D. 4个

    B 【解析】在-8，0，-32，-（-5.7）中负数是-8，-32，共计负数的个数有2个． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：山东省东营市河口区2017－2018学年度第一学期期末考试七年级数学试卷 题型：单选题

    如图，动点P在平面直角坐标系中按图中箭头所示的方向运动，第1次从原点运动到（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过2017次运动后，动点P的坐标为( )

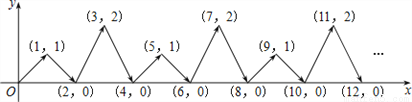
    A. （2017，1） B. （2017，0） C. （2017，2） D. （2016，0）

    A 【解析】根据动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点(1，1)，第2次接着运动到点(2，0)，第3次接着运动到点(3，2)，∴第4次运动到点(4，0)，第5次接着运动到点(5，1)，…，∴横坐标为运动次数，经过第2017次运动后，动点P的横坐标为2017，纵坐标为1，0，2，0，每4次一轮，∴经过第2017次运动后，动点P的纵坐标为：2017÷4＝504余1，...

    查看答案和解析>>

    科目：初中数学 来源：江西省赣州市2017-2018学年七年级（上）期中数学试卷 题型：解答题

    已知a，b，c在数轴上的位置如图所示，

    求|a+b|﹣3|b+c|+2|a﹣b|﹣|c﹣b|的值．

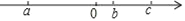
    －3a－b－4c 【解析】试题分析：先根据a、b、c在数轴上的位置确定a、b、c符号和大小关系，然后依据加法和减法法则确定a＋b、b＋c、a－b、c－b的符号，再利用绝对值的性质去掉绝对值，最后去括号、合并同类项即可得出答案． 试题解析： 解：由数轴可知a＜0＜b＜c，且｜a｜＞｜b｜， 所以a＋b＜0，b＋c＞0，a－b＜0，c－b＞0， 所以｜a＋b｜＝－(a＋b...

    查看答案和解析>>

    同步练习册答案