
阅读下面的计算过程:
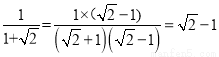 ;
;
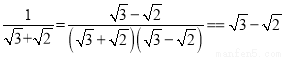 ;
;
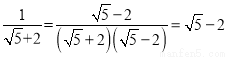 …
…
根据以上信息,解答下面的问题:
(1)化简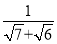 = (直接写出结果);
= (直接写出结果);
(2)化简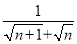 = (n为正整数,直接写出结果);
= (n为正整数,直接写出结果);
(3)利用上面所提供的解法计算:
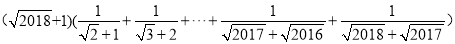
科目:初中数学 来源:北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型:单选题
长为9,6,5,4的四根木条,选其中三根组成三角形,选法有( )
A. 1种 B. 2种 C. 3种 D. 4种
C 【解析】试题分析:因为6,5,4; 9,6,5; 9,6,4.均符合三角形三边之间的关系,即三角形的两边之和大于第三边,两边之差小于第三边. 故选C.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型:单选题
要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
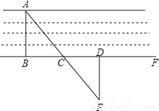
A. 边角边 B. 角边角 C. 边边边 D. 边边角
B 【解析】试题分析:由已知可以得到∠ABC=∠BDE=90°,又CD=BC,∠ACB=∠DCE,由此根据角边角即可判定△EDC≌△ABC. 故选:B.查看答案和解析>>
科目:初中数学 来源:内蒙古包头市青山区2017-2018学年八年级(上)期末数学试卷 题型:单选题
如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠BAC=60°,∠ABE=25°,则∠DAC的大小是( )
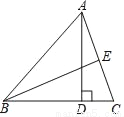
A. 15° B. 20° C. 25° D. 30°
B 【解析】试题解析:∵BE平分∠ABC, ∴∠ABC=2∠ABE=2×25°=50°, ∵AD是BC边上的高, ∴∠BAD=90°﹣∠ABC=90°﹣50°=40°, ∴∠DAC=∠BAC﹣∠BAD=60°﹣40°=20°. 故选B.查看答案和解析>>
科目:初中数学 来源:内蒙古包头市青山区2017-2018学年八年级(上)期末数学试卷 题型:单选题
下列计算正确的是( )
A. 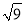 =±3 B.
=±3 B. 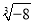 =﹣2 C.
=﹣2 C. 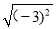 =﹣3 D.
=﹣3 D. 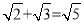
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
已知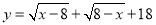 ,求代数式
,求代数式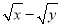 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB的度数为_____.
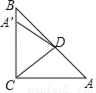
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下5.3.1 等腰三角形的性质 同步练习 题型:单选题
等腰三角形是轴对称图形,它的对称轴有( )
A. 1条 B. 2条 C. 1条或3条 D. 不确定
C 【解析】试题解析: 若等腰三角形只有两边相等,则有一条对称轴, 若等腰三角形的三边都相等,即等边三角形,则有三条对称轴, 所以,它的对称轴有1条或3条. 故选C.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.3.2 用“角边角、角角边”判定三角形全等 同步练习 题型:解答题
如图,已知∠CAB=∠DBA,∠CBD=∠DAC.求证:BC=AD.
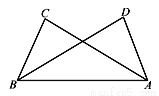
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com