
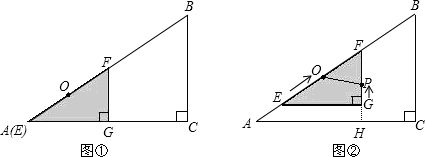
| ��ͼ����������״��ȫ��ͬ��ֱ��������ABC��EFG������һ�𣨵�A���E�غϣ�����֪AC=8cm��BC=6cm����C=90�㣬EG=4cm����EGF=90�㣬O�ǡ�EFGб���ϵ��е㣮 ��ͼ����������EFG��ͼ��λ�ó�������1cm/s���ٶ�������AB����ƽ�ƣ��ڡ�EFGƽ�Ƶ�ͬʱ����P�ӡ�EFG�Ķ���G��������1cm/s���ٶ���ֱ�DZ�GF�����F�˶�������P�����Fʱ����Pֹͣ�˶�����EFGҲ��ֹ֮ͣƽ�ƣ����˶�ʱ��Ϊx��s����FG���ӳ��߽�AC��H���ı���OAHP�����Ϊy��cm2���������ǵ�P��G��F�غϵ�������� |
 |
| ��1����xΪ��ֵʱ��OP��AC�� ��2����y��x֮��ĺ�����ϵʽ����ȷ���Ա���x��ȡֵ��Χ�� ��3���Ƿ����ijһʱ�̣�ʹ�ı���OAHP������ABC����ı�Ϊ13��24�����ڣ����x��ֵ���������ڣ�˵�����ɣ����ο����ݣ�1142=12996��1152=13225��1162=13456��4.42=19.36��4.52=20.25��4.62=21.16�� |
| �⣺��1����Rt��EFG��Rt��ABC ��  �� �� ��FG=  =3cm =3cm�ߵ�PΪFG���е�ʱ��OP��EG��EG��AC ��OP��AC ��x=  = = ��3=1.5��s�� ��3=1.5��s���൱xΪ1.5sʱ��OP��AC�� ��2����Rt��EFG�У��ɹ��ɶ�����EF=5cm ��EG��AH ���EFG�ס�AFH ��  ��AH=  ��x+5����FH= ��x+5����FH= ��x+5�� ��x+5������O��OD��FP������ΪD �ߵ�OΪEF�е� ��OD=  EG=2cm EG=2cm��FP=3��x ��S�ı���OAHP=S��AFH��S��OFP =   AH AH FH�� FH��  OD OD FP FP=    ��x+5�� ��x+5��  ��x+5���� ��x+5���� ��2����3��x�� ��2����3��x��=  x2+ x2+ x+3��0��x��3���� x+3��0��x��3������3���������ijһʱ��x��ʹ���ı���OAHP������ABC����ı�Ϊ13��24 ��S�ı���OAHP=  ��S��ABC ��S��ABC��  x2+ x2+ x+3= x+3= �� �� ��6��8 ��6��8��6x2+85x��250=0 ���x1=  ��x2=�� ��x2=�� ����ȥ�� ����ȥ����0��x��3 �൱x=  ��s��ʱ���ı���OAHP������ABC����ı�Ϊ13��24�� ��s��ʱ���ı���OAHP������ABC����ı�Ϊ13��24�� |
 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����2�¡����κ������п��⼯��42����2.7 �������Ƕ��٣������棩 ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����2�¡����κ������п��⼯��45����2.3 ���κ�����Ӧ�ã������棩 ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����2�¡����κ������п��⼯��42����2.4 ���κ�����Ӧ�ã������棩 ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������24�� ͼ�ε����ơ�2009�굥Ԫ�����Ծ��������棩 ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com