练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（　　）

    A. B. C. D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省淄博市2017届九年级下学期期中考试数学试卷 题型：解答题

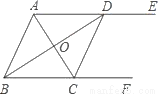
    如图，AE∥BF，AC平分∠BAE，且交BF于点C，BD平分∠ABF，且交AE于点D，AC与BD相交于点O，连接CD

    （1）求∠AOD的度数；

    （2）求证：四边形ABCD是菱形．

    【答案】（1）∠AOD=90°；（2）证明见解析.

    【解析】试题分析：（1）首先根据角平分线的性质得到∠DAC=∠BAC，∠ABD=∠DBC，然后根据平行线的性质得到∠DAB+∠CBA=180°，从而得到∠BAC+∠ABD=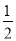（∠DAB+∠ABC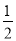）=×180°=90°，得到答案∠AOD=90°；

    （2）根据平行线的性质得出∠ADB=∠DBC，∠DAC=∠BCA，根据角平分线定义得出∠DAC=∠BAC，∠ABD=∠DBC，求出∠BAC=∠ACB，∠ABD=∠ADB，根据等腰三角形的判定得出AB=BC=AD，根据平行四边形的判定得出四边形ABCD是平行四边形，即可得出答案．

    试题解析：（1）∵AC、BD分别是∠BAD、∠ABC的平分线，∴∠DAC=∠BAC，∠ABD=∠DBC，∵AE∥BF，∴∠DAB+∠CBA=180°，∴∠BAC+∠ABD=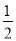（∠DAB+∠ABC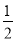）=×180°=90°，∴∠AOD=90°；

    （2）证明：∵AE∥BF，∴∠ADB=∠DBC，∠DAC=∠BCA，∵AC、BD分别是∠BAD、∠ABC的平分线，∴∠DAC=∠BAC，∠ABD=∠DBC，∴∠BAC=∠ACB，∠ABD=∠ADB，∴AB=BC，AB=AD

    ∴AD=BC，∵AD∥BC，∴四边形ABCD是平行四边形，∵AD=AB，∴四边形ABCD是菱形．

    考点：菱形的判定．

    【题型】解答题
    【结束】
    22

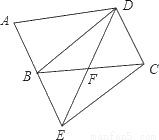
    如图，将?ABCD的边AB延长到点E，使BE=AB，连接DE，交边BC于点F．

    （1）求证：△BEF≌△CDF；

    （2）连接BD、CE，若∠BFD=2∠A，求证：四边形BECD是矩形．

    查看答案和解析>>

    科目：初中数学 来源：福建省2016-2017学年八年级下学期期中考试数学试卷 题型：单选题

    已知点A（3，-2），将点A向左平移4个单位长度得到点B，则点B在（ ）

    A. 第一象限； B. 第二象限； C. 第三象限； D. 第四象限．

    查看答案和解析>>

    科目：初中数学 来源：湖北省孝感市云梦县2018届九年级上学期期中考试数学试卷（WORD版） 题型：填空题

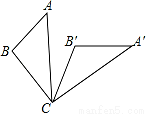
    将△ABC绕着点C顺时针方向旋转60°后得到△A′B′C′，若∠A=50°，∠B′=100°，则∠BCA′的度数是_____．

    查看答案和解析>>

    科目：初中数学 来源：湖北省孝感市云梦县2018届九年级上学期期中考试数学试卷（WORD版） 题型：单选题

    我们知道方程x2+2x–3=0的解是x1=1，x2=–3，现给出另一个方程（2x+3）2+2（2x+3）–3=0，它的解是( )

    A. x1=1，x2=3 B. x1=1，x2=–3

    C. x1=–1，x2=3 D. x1=–1，x2=–3

    查看答案和解析>>

    科目：初中数学 来源：苏科版南京栖霞区2017-2018学年度上期九年级数学期末模拟试卷 题型：解答题

    随着绿城南宁近几年城市建设的快速发展，对花木的需求量逐年提高．某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润y1与投资量x成正比例关系，如图①所示；种植花卉的利润y2与投资量x成二次函数关系，如图②所示（注：利润与投资量的单位：万元）

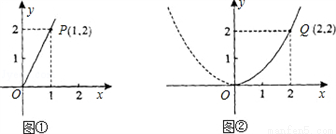
    （1）分别求出利润y1与y2关于投资量x的函数关系式；

    （2）如果这位专业户以8万元资金投入种植花卉和树木，他至少获得多少利润，他能获取的最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源：苏科版南京栖霞区2017-2018学年度上期九年级数学期末模拟试卷 题型：填空题

    如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象，观察图象写出y2≥y1时，x的取值范围__．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年度陕西省西安市第一学期九年级数学第一阶段模拟测试卷及参考答案 题型：解答题

    用两个全等的等边△ＡＢＣ和△ADC，在平面上拼成菱形ABCD，把一个含60°角的三角尺与这个菱形重合，使三角尺有两边分别在AB、AC上，将三角尺绕点A按逆时针方向旋转.

    (1)如图1，当三角尺的两边与BC、CD分别相交于点E、F时，观察或测量BE，CF的长度，你能得出什么结论？证明你的结论。

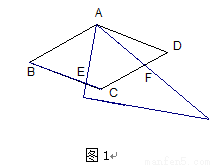
    (2)如图2，当三角尺的两边与BC、CD的延长线分别交于E、F时，你在（1）中的结论还成立吗？请说明理由。

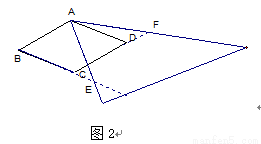
    查看答案和解析>>

    科目：初中数学 来源：河北省唐山市九年级上数学期末复习检测题 题型：填空题

    如图，对称轴平行于y轴的抛物线与x轴交于(1，0)，(3，0)两点，则它的对称轴为_________.

    查看答案和解析>>

    同步练习册答案