
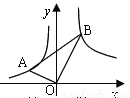
如图,在Rt△ABO中,∠AOB=90°,且OB=2AO,点A在反比例函数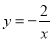 的图象上,点B比在反比例函数
的图象上,点B比在反比例函数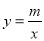 的图象上,则m是( )
的图象上,则m是( )
A. 4 B. 6 C. -8 D. 8
D 【解析】试题解析:如图,设点A的坐标是(a,b), 因为点A在函数的图象上,则ab=-2, 则AC=b,OC=-a, ∵∠AOB=90°, ∴∠AOC+∠BOD=∠AOC+∠CAO=90°, ∠CAO=∠BOD, ∴△ACO∽△BDO, ∴ ∴OD=2b,BD=-2a, ∴B(2b,-2a), ∵点B比在反比例函数的图象上, ...科目:初中数学 来源:湖北省武汉市洪山区2018届九年级(上)期中数学试卷 题型:单选题
如图,一座石拱桥是圆弧形其跨度AB=24米,半径为13米,则拱高CD为( )
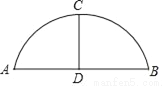
A. 3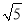 米 B. 5米 C. 7米 D. 8米
米 B. 5米 C. 7米 D. 8米
查看答案和解析>>
科目:初中数学 来源:四川省西昌市2017-2018学年九年级数学(上)期末模拟试卷 题型:解答题
已知一抛物线与x轴的交点是A(-2,0)、B(1,0),且经过点C(2,8),求该抛物线的解析式.
y=2x2+2x-4 【解析】试题分析:由抛物线与x轴的交点是A(-2,0),B(1,0),且经过点C(2,8),设解析式为一般式或交点式用待定系数法求得二次函数的解析式. 试题解析:设这个抛物线的解析式为y=ax2+bx+c. 由已知,抛物线过A(?2,0),B(1,0),C(2,8)三点, 得, ①+③得,8a+2c=8,即4a+c=4④, ①+②×2得6a...查看答案和解析>>
科目:初中数学 来源:重庆市2018届2017年秋期期末冲刺卷 题型:解答题
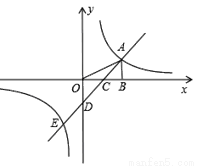
如图,在平面直角坐标系中,点A是反比例函数y=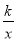 (k≠0)图象上一点,AB⊥x轴于B点,一次函数y=ax+b(a≠0)的图象交y轴于D(0,-2),交x轴于C点,并与反比例函数的图象交于A,E两点,连接OA,若△AOD的面积为4,且点C为OB中点.
(k≠0)图象上一点,AB⊥x轴于B点,一次函数y=ax+b(a≠0)的图象交y轴于D(0,-2),交x轴于C点,并与反比例函数的图象交于A,E两点,连接OA,若△AOD的面积为4,且点C为OB中点.
(1)分别求双曲线及直线AE的解析式;
(2)若点Q在双曲线上,且S△QAB=4S△BAC,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源:重庆市2018届2017年秋期期末冲刺卷 题型:填空题
在-3、-2、-1、0、1、2这六个数中,随机取出一个数,记为a,那么使得关于x的反比例函数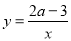 经过第二、四象限,且使得关于x的方程
经过第二、四象限,且使得关于x的方程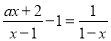 有整数解的概率为____.
有整数解的概率为____.
查看答案和解析>>
科目:初中数学 来源:重庆市2018届2017年秋期期末冲刺卷 题型:单选题
已知圆锥的侧面积展开图的面积是15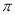 cm2,母线长是5cm,则圆锥的底面半径为( )
cm2,母线长是5cm,则圆锥的底面半径为( )
A. 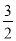 cm B. 3cm C. 4cm D. 6cm
cm B. 3cm C. 4cm D. 6cm
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初一上期中数学试卷数学试卷 题型:解答题
数轴上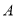 、
、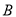 对应的数分别为
对应的数分别为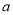 、
、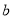 ,且
,且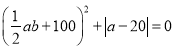 ,点
,点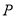 是数轴上一个动点.
是数轴上一个动点.
(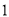 )求
)求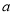 、
、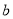 的值,并在数轴上标出
的值,并在数轴上标出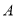 、
、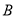 的位置.
的位置.
(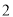 )数轴上一点
)数轴上一点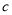 距离
距离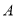 点
点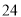 个单位长度,其对应的数
个单位长度,其对应的数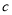 满足
满足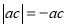 ,求点
,求点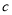 对应的数.
对应的数.
(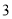 )动点
)动点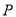 从原点开始第一次向左移动
从原点开始第一次向左移动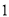 个单位长度,第二次向右移动
个单位长度,第二次向右移动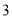 个单位长度,第三次向左移动
个单位长度,第三次向左移动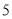 个单位长度,第四次向右移动
个单位长度,第四次向右移动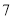 个单位长度,
个单位长度,  ,点
,点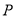 能移动到与
能移动到与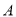 或者
或者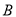 重合的位置吗?若能,试探索第几次移动时重合;若不能,请说明理由.
重合的位置吗?若能,试探索第几次移动时重合;若不能,请说明理由.
(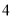 )在(
)在(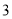 )的条件下,求点
)的条件下,求点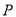 移动
移动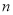 次后所表示的数.
次后所表示的数.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初一上期中数学试卷数学试卷 题型:单选题
如图,数轴上的点A所表示的数为k,化简|k|+|1﹣k|的结果为( )

A. 1 B. 2k﹣1 C. 2k+1 D. 1﹣2k
B 【解析】由数轴可知:k>1,∴k>0,1?k<0. ∴|k|+|1?k|=k?1+k=2k?1. 故选B.查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试七年级数学试卷 题型:填空题
月球的半径约为1738000米,1738000这个数用科学记数法表示为___________.
1.738×106 【解析】试题分析:将1738000用科学记数法表示为1.738×106.故答案为:1.738×106.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com