
甲、乙两人同时从同一地点出发,甲往北偏东60°的方向走了12 km,乙往南偏东30°的向走了5 km,这时甲、乙两人相距___________km
13 【解析】试题解析:如图所示, ∵甲往北偏东60°的方向走了12km,乙往南偏东30°的向走了5km, ∴∠AOB=90°, ∴AB==13(km). 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:山东省日照市莒县2017-2018学年七年级(上)期中数学试卷 题型:单选题
计算﹣22+3的结果是( )
A. 7 B. 5 C. ﹣1 D. ﹣5
C 【解析】试题解析:﹣22+3=﹣4+3=﹣1. 故选C.查看答案和解析>>
科目:初中数学 来源:吉林省长春市五校2018届九年级(上)期中数学试卷 题型:解答题
解下列方程:
(1)x2﹣3x=1.
(2)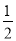 (y+2)2﹣6=0.
(y+2)2﹣6=0.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期苏州市八年级数学期末复习综合检测卷 题型:解答题
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点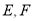 分别在正方形
分别在正方形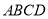 的边
的边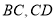 上,
上, 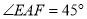 ,连接
,连接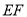 ,则
,则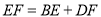 ,试说明理由.
,试说明理由.
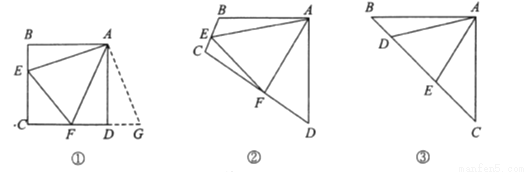
(1)思路梳理
因为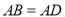 ,所以把
,所以把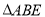 绕点
绕点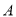 逆时针旋转90°至
逆时针旋转90°至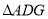 ,可使
,可使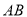 与
与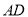 重合.因为
重合.因为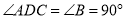 ,所以
,所以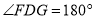 ,点
,点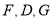 共线.
共线.
根据 ,易证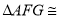 ,得
,得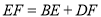 .请证明.
.请证明.
(2)类比引申
如图②,四边形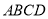 中,
中, 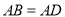 ,
, 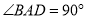 ,点
,点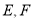 分别在边
分别在边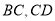 上,
上, 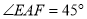 .若
.若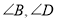 都不是直角,则当
都不是直角,则当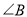 与
与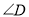 满足等量关系时,
满足等量关系时, 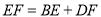 仍然成立,请证明.
仍然成立,请证明.
(3)联想拓展
如图③,在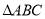 中,
中, 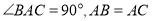 ,点
,点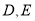 均在边
均在边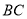 上,且
上,且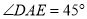 .猜想
.猜想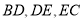 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期苏州市八年级数学期末复习综合检测卷 题型:解答题
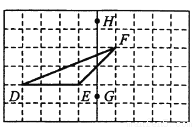
如图,在正方形网格上有一个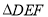 .
.
(1)画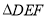 关于直线
关于直线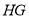 的轴对称图形.
的轴对称图形.
(2)画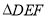 的
的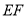 边上的高.
边上的高.
(3)若网格上的最小正方形边长为1,求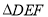 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期苏州市八年级数学期末复习综合检测卷 题型:填空题
如果等腰三角形的底角是50°,那么这个三角形的顶角的度数是___________
80° 【解析】试题解析:180°-50°×2 =180°-100° =80°. 故这个三角形的顶角的度数是80°.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期苏州市八年级数学期末复习综合检测卷 题型:单选题
在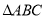 中,
中, 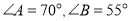 ,则
,则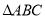 是( )
是( )
A. 钝角三角形 B. 等腰三角形
C. 等边三角形 D. 等腰直角三角形
B 【解析】试题解析:∵在△ABC中,∠A=70°,∠B=55°, ∴∠C=180°-∠A-∠B=55°, ∴∠B=∠C, ∴△ABC是等腰三角形. 故选B.查看答案和解析>>
科目:初中数学 来源:河北省秦皇岛市卢龙县2017-2018学年八年级(上)期中数学试卷 题型:单选题
下列平面图形中,不是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年第一学期初一数学期末调研测试卷(含答案) 题型:填空题
若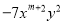 与
与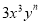 是同类项,则
是同类项,则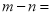 ________.
________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com