
 如图,设图中的每个小正方形的边长为1,
如图,设图中的每个小正方形的边长为1, 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,设图中的每个小正方形的边长为1,
如图,设图中的每个小正方形的边长为1,查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
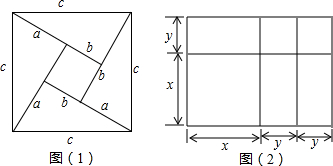
科目:初中数学 来源:湖北省黄冈市黄梅县实验中学2010-2011学年八年级下学期期中考试数学试题 题型:059
请阅读下列材料:
问题:现有5个边长为1的正方形,排列形式如图1,请把它们分割后拼接成一个新的正方形,要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.

小东同学的做法是:设新正方形的边长为x(x>0).依题意,割补前后图形的面积相等,有x2=5,解得x=![]() ,由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长.于是,画出如图2所示的分割线,拼出如图3所示的新正方形.
,由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长.于是,画出如图2所示的分割线,拼出如图3所示的新正方形.
请你参考小东同学的做法,解决如下问题:
现有10个边长为1的正方形,排列形式如图4,请把它们分割后拼接成一个新的正方形,要求:在图4中画出分割线并在图5的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.

说明:直接画出图形不要求分析过程
查看答案和解析>>
科目:初中数学 来源:河北省中考真题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com