练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列去括号中正确的是（   ）

    A. 3x﹣（2x﹣1）=4，得3x﹣2x﹣1=4 B. ﹣4（x+1）+3=x，得﹣4x+4+3=x

    C. 2x+7（x﹣1）=﹣9x+5，得2x﹣7x﹣7=﹣9x+5 D. 3﹣[2x﹣4（x+1）]=2，得3﹣2x+4x+4=2

    D 【解析】A、3x﹣（2x﹣1）=4，得3x﹣2x+1=4，错误； B、﹣4（x+1）+3=x，得﹣4x﹣4+3=x，错误；C、2x+7（x﹣1）=﹣9x+5，得2x+7x﹣7=﹣9x+5，错误；D、3﹣[2x﹣4（x+1）]=2，得3﹣2x+4x+4=2，正确， 故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：内蒙古赤峰市宁城县2018届九年级上学期期末数学试卷 题型：解答题

    阅读理解题：

    按照一定顺序排列着的一列数称为数列，排在第一位的数称为第1项，记为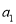，依次类推，排在第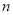位的数称为第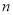项，记为．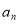

    一般地，如果一个数列从第二项起，每一项与它前一项的比等于同一个常数，那么这个数列叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母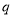表示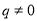（）．如：数列1，3，9，27，…为等比数列，其中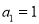，公比为．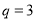

    则：（1）等比数列3，6，12，…的公比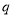为_____________，第4项是________________．

    （2）如果一个数列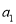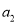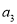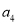， ， ， ，…是等比数列，且公比为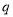，那么根据定义可得到：

    ， ， ，…… ．

    ∴， ， ，

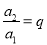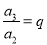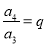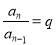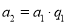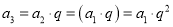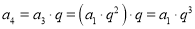    由此可得：an=____________________（用a1和q的代数式表示）

    （3）若一等比数列的公比q=2，第2项是10，请求它的第1项与第4项．

    2 an=a1qn-1 5， 40 【解析】试题分析：（1）根据等比数列的定义可得； （2）由数列中的每一项等于首项乘以公比的序数减一次方可得； （3）根据定义先求得首项，再根据通项公式即可得. 试题解析：：（1）根据题意知公比q=6÷3=2，第4项是12×2=24； （2）根据定义我们可依次写出这个数列的每一项：a1，a1q，a1•q2，a1•q3，…．由此可得第n项an=...

    查看答案和解析>>

    科目：初中数学 来源：广东省初中部2017-2018学年第一学期期末模拟测试七年级数学试卷 题型：单选题

    已知代数式x＋2y的值是3，则代数式2x＋4y＋1的值是（ ）

    A. 1 B. 4 C. 7 D. 不能确定

    C 【解析】试题分析：将所求代数式化成，再将代入，可求得.

    查看答案和解析>>

    科目：初中数学 来源：贵州省贵阳市2017-2018学年七年级（上）期末模拟数学试卷 题型：填空题

    去括号，并合并同类项：3x+1﹣2（4﹣x）=________．

    5x﹣7 【解析】3x+1﹣2（4﹣x）=3x+1﹣8+2x=5x﹣7， 故答案为：5x﹣7．

    查看答案和解析>>

    科目：初中数学 来源：贵州省贵阳市2017-2018学年七年级（上）期末模拟数学试卷 题型：单选题

    买一个足球需要m元，买一个篮球需要n元，则买4个足球、7个篮球共需要（　　）元．

    A. 4m+7n B. 28mn C. 7m+4n D. 11mn

    A 【解析】已知一个足球需要m元，买一个篮球需要n元，可得买4个足球、7个篮球共需要（4m+7n）元，故选A.

    查看答案和解析>>

    科目：初中数学 来源：云南省2016-2017学年七年级上学期期末考试数学试卷 题型：解答题

    如图，∠AOB=35°，∠BOC=90°，OD是∠AOC的平分线，求∠BOD的度数．

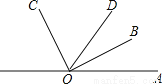
    27.5°． 【解析】 试题分析：先求出∠AOC的度数，再由角平分线的定义得出∠AOD的度数，根据∠BOD=∠AOD﹣∠AOB即可得出结论． 【解析】 ∵∠AOB=35°，∠BOC=90°， ∴∠AOC=35°+90°=125°． ∵OD是∠AOC的平分线， ∴∠AOD=∠AOC=62.5°， ∴∠BOD=∠AOD﹣∠AOB=62.5°﹣35°=27.5...

    查看答案和解析>>

    科目：初中数学 来源：云南省2016-2017学年七年级上学期期末考试数学试卷 题型：填空题

    如图，下面是用火柴棍摆的正方形，请你仔细观察第n个图形中共有__________根火柴棍（用含n的式子表示）.

    4 + 3（n-1）或 3n + 1 【解析】从图中可知n每增加1，就要多用3根火柴棍， n=1，所用火柴棍3+1=4根， n=2，所用火柴棍2×3+1=7根， n=3，所用火柴棍3×3+1=10根， n=4，所用火柴棍4×3+1=13根， … 第n个图形中就该有火柴棍3n+1， 故答案为：3n+1．

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016-2017学年七年级上学期期末考试数学试卷 题型：解答题

    如图，O为直线AB上一点，OD平分∠AOC，∠DOE=90°．

    （1）若∠AOC=50°，求出∠BOD的度数；

    （2）试判断OE是否平分∠BOC，并说明理由．

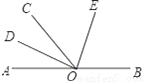
    （1）155°；（2）证明见解析． 【解析】试题分析：（1）已知OD平分∠AOC，根据角平分线的定义求得∠AOD的度数，再由平角的定义求得∠BOD的度数；（2）已知OD平分∠AOC，根据角平分线的定义求得∠AOD的度数，再求得∠COE和∠BOE的度数，即可判断OE是否平分∠BOC. 试题解析： （1）∵OD平分∠AOC ∴∠AOD=∠AOC = ∴∠B...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省葫芦岛市建昌县2017-2018学年八年级上学期期末测评数学试卷 题型：单选题

    将一副直角三角扳如图放置，使含30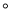角的三角板的直角边和含45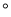角的三角扳的一条直角边重合，则∠1的度数为（　　）

    A. 55 B. 50 C. 65 D. 75

    D 【解析】 ∵∠2=90°?45°=45°， ∴∠3=∠2=45°， ∴∠1=∠3+30°=45°+30°=75°. 故选：D.

    查看答案和解析>>

    同步练习册答案