
减去2﹣x等于3x2﹣x+6的整式是( )
A. 3x2﹣2x+8 B. 3x2+8 C. 3x2﹣2x﹣4 D. 3x2+4
A 【解析】试题解析:所求整式为: 故选A.科目:初中数学 来源:2017年安徽省中考数学模拟试卷 题型:单选题
在娱乐节目“墙来了!”中,参赛选手背靠水池,迎面冲来一堵泡沫墙,墙上有人物造型的空洞.选手需要按墙上的造型摆出相同的姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一块几何体恰好能以右图中两个不同形状的“姿势” 分别穿过这两个空洞,则该几何体为( )
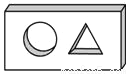
A. 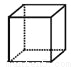 B.
B. 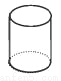 C.
C. 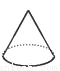 D.
D. 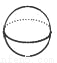
查看答案和解析>>
科目:初中数学 来源:江苏省徐州市区联校2017-2018学年七年级上学期期中联考数学试卷 题型:填空题
若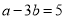 ,则
,则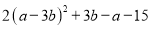 =________.
=________.
查看答案和解析>>
科目:初中数学 来源:山东省诸城市2017-2018学年七年级上学期第二次月考数学试卷 题型:解答题
先化简,再求值:4x2y﹣[6xy﹣2(4xy﹣2)+2x2y]+1,其中x=﹣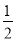 ,y=1.
,y=1.
查看答案和解析>>
科目:初中数学 来源:山东省诸城市2017-2018学年七年级上学期第二次月考数学试卷 题型:填空题
单项式﹣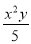 的系数是________,次数是________.
的系数是________,次数是________.
查看答案和解析>>
科目:初中数学 来源:山东省诸城市2017-2018学年七年级上学期第二次月考数学试卷 题型:单选题
如果3x2myn+1与﹣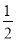 x2ym+3是同类项,则m,n的值为( )
x2ym+3是同类项,则m,n的值为( )
A. m=﹣1,n=3 B. m=1,n=3 C. m=﹣1,n=﹣3 D. m=1,n=﹣3
B 【解析】【解析】 ∵3x2myn+1与﹣x2ym+3是同类项,∴2m=2,n+1=m+3,解得m=1,n=3.故选B.查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型:解答题
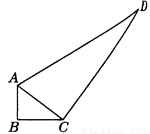
一个零件的形状如图所示,工人师傅按规定做得∠B=90°,
AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
【答案】面积等于36
【解析】试题分析:利用勾股定理求AC,再利用勾股定理逆定理求∠ACB=90°,分别求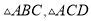 的面积.
的面积.
试题解析:
 ∠B=90°,AB=3,BC=4,AC=
∠B=90°,AB=3,BC=4,AC=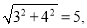
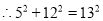 =169,
=169,
所以∠ACD=90°,
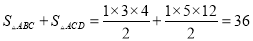 .
.
所以面积是36.
【题型】解答题
【结束】
22
如图,在所给正方形网格(每个小网格的边长是1)图中完成下列各题.
(1)格点△ABC(顶点均在格点上)的面积=_________;
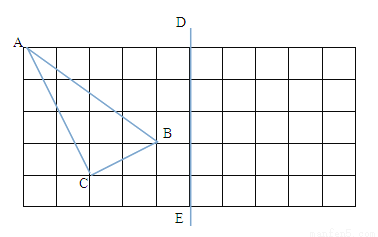
(2)画出格点△ABC关于直线DE对称的△A1B1C1;
(3)在DE上画出点P,使PB+PC最小,并求出这个最小值.
(1)面积等于5(2)图形见解析(3)最小值是根号17 【解析】试题分析:(1)利用勾股定理求出三角形边长,并证明是直角三角形求面积.(2)画出A,B,C的对称点A1,B2,C3,连接三角形.(3)利用对称利用两点之间直线最短求最小值. 试题解析: (1)分别利用勾股定理求得AC=2,AB=,BC=, ,所以∠ACB=90°,面积等于=5. (2)画出A,B,C的对称点A1...查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型:单选题
等腰三角形的周长为15cm,其中一边长为3cm.则该等腰三角形的腰长为 ( )
A. 3cm B. 6cm C. 3cm或6cm D. 3cm或9cm
B 【解析】试题解析:当3cm是底时,则腰长是(15-3)÷2=6(cm),此时能够组成三角形; 当3cm是腰时,则底是15-3×2=9(cm),此时3+3<9,不能组成三角形,应舍去. 故选B.查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:填空题
已知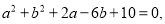 则
则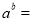 _______
_______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com