

| 解:(1)E(3,1);F(1,2); | |
(2)在Rt△EBF中,∠B=90°,所以EF= , ,设点P的坐标为(0,n),其中n>0, 因为顶点F(1,2), 所以设抛物线的解析式为y=a(x-1)2+2(a≠0), ①如图1,当EF=PF时,EF2=PF2, 所以12+(n-2)2=5,解得n1=0(舍去),n2=4, 所以P(0,4), 所以4=a(0-1)2+2,解得a=2, 所以抛物线的解析式为y=2(x-1)2+2; ②如图2,当EP=FP时,EP2=FP2, 所以(2-n)2+1=(1-n)2+9,解得n=-  (舍去); (舍去);③当EF=EP时,EP=  <3,这种情况不存在。 <3,这种情况不存在。综上所述,符合条件的抛物线为y=2(x-1)2+2。 |
  |
|
(3)存在点M、N,使得四边形MNFE的周长最小。 |
 |


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
 A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动.
A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动.查看答案和解析>>
科目:初中数学 来源: 题型:
 10、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为
10、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为查看答案和解析>>
科目:初中数学 来源: 题型:
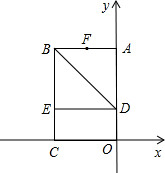 直角坐标系.已知OA=6,OC=4,在OA上取一点D,将△BDA沿BD翻折,点A恰好落在BC边上的点E处.
直角坐标系.已知OA=6,OC=4,在OA上取一点D,将△BDA沿BD翻折,点A恰好落在BC边上的点E处.查看答案和解析>>
科目:初中数学 来源: 题型:
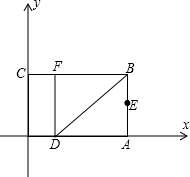 系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com